
because det(L) = 1; the right hand side is easily computed as the product of all diagonal elements of U multiplied with the determinant of the permutation matrix P (which is +1 for an even permutation and is -1 for an odd permutation). This is more efficient than calculating the determinant of A because the determinant of a (upper or lower) triangular matrix is the product of its diagonal elements.
A small example:
 due the calculations are linneardet(A-lambdasubi*I=C)=0->in a base B we obtain the diagonal matrix ,B*C*B^-1=I(2 0 0 0.................................0) ( )=(-(2^n)-1 n=0(0 4 0 0..................................0) ---- (-2^n)-2=0(----------------------------...............0) ... ...C=((0 0 2^(a-1) 00..,00.....................0) X= (2^(n-1)-(2^n))=0=-1/2=lambdaN for all n
due the calculations are linneardet(A-lambdasubi*I=C)=0->in a base B we obtain the diagonal matrix ,B*C*B^-1=I(2 0 0 0.................................0) ( )=(-(2^n)-1 n=0(0 4 0 0..................................0) ---- (-2^n)-2=0(----------------------------...............0) ... ...C=((0 0 2^(a-1) 00..,00.....................0) X= (2^(n-1)-(2^n))=0=-1/2=lambdaN for all n
(0 0 3 0 0 --...............0)
( ----------------------------------------
(0 0 0 3^4 0 ....................0)(0 0 0 0 0 3^b 0..0..00)( ........................................ )(0...... ...pi^k................0). (..................................................0)(0....----------..........................pn^n) , det(C)=p(n+1)-1 even,pair number=2^a*3^b*5^c*pn^n ,it conforms the system of equations: det(C-2^a*I)=0..det(C-3^b*I)=0
we also can use the conjecture of coldbach pi+pm=((p(n+1)-1))*(1/(p(n+1)-1)^n)=even(1/(p(n+1)-1)^n)*(pi+pm)=((p(n+1)-1))->(1/(p(n+1)-1)^n)*(2^a*3^b*5^c*p(i-1)^(i-1)+2^a*3^b*5^c*p(m-1)^(m-1)) q,c,dseeing at another perspective
q,c,dseeing at another perspective
(1 0 0 ) (0 0 1)
C=(2 0 0...) C-1=(0 0 1/2)
(0 4 0...) (0 1/4 0)
(0 0 8...) (1/8 0 0)
(......... ) ............
(0 0 0 2^a) (1/2^a 0 0)
Det[(C)tensor product x Ntimes x C x (D) .. Ntimes D x ... N x Ntimes x..xN]
= ((lambda1=-1=(1/(2*2^2*2^4*2^3*..2^N)^(2*2^2*2^4*2^3*..2^N))+1)*(lambda2=
-1=1/(3^2*3^3*3^4*..*3^N)^ (3^2*3^3*3^4*..*3^N))+1)*...*(lambdaN=
-1=1/(pN*pN^2*pN^3*..*P^N)^(pN*pN^2*pN^3*..*P^N))+1)=zeta(S)=0

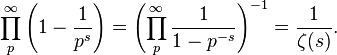 =((p^S)-1)/p^S=
=((p^S)-1)/p^S=
Det(C-1)*Det[(C-1)tensor product x (D-1)x..x(N-1)]*Det(1/C^t (tensor product=x) 1/D^t ) x 1/E^t x..1/(N-1)^t)*
Det(CxDx..xN)*(C^-1xD^-1x..xN^-1)=Ix..Ntimes..xI lambdai=1^N just need to apply in a recurrent form conjecture of coldback prime1+prime2=even so we also can use the conjecture of coldbach pi+pm=((p(n+1)-1))*(1/(p(n+1)-1)^n)=even develop and obtain final soilution
Relation to the Riemann zeta function
Some derivatives of fractional harmonic numbers are given by:And using Maclaurin series, we have for x<1 :where ζ(n) is the Riemann zeta function.
C=(C/2-2*lambda*IxIxI..I) ->lambdasubi=2^i
D=(3 0 0...)
(0 9 0...)
(0 0 27..)
.....
(0 0 0 3^b)
D=D/3-3lambdaIxIxI..I .>lambdasubj=3^j
E=(5 0 0...0)
(0 0 25..0)
...........
(0 0 0 5^c)
....
N=(pn 0 0 ..0)
(0 pn^2 0..0)
. ................
(0 0 0 pn^z)
|((C tensor product D tensor product E ... tensor product N)-(lambda=(2^a*3^b*5^c*p(i-1)^(i-1) ( I tensor product I ... tensor product I) ....|=0->lambdasubi=pi=PA=LU->PA=I*BB*C=I*B->C=B^-1*B=B^t*B/det|B|->det(C) normalized= p(n+1)-1=(2^a/(2^a*3^b*5^c*pn^n))*(3^b/(2^a*3^b*5^c*pn^n))*..*((pn^n/(2^a*3^b*5^c*pn^n))=(p(n+1)-1)=((p(n+1)-1))*(1/(p(n+1)-1)^n)det(A-lambdasubi*I=C)=0 Method to obtain prime numbers:det|A-lambdasubi*I|=0A=(1 111111111111111111..(2 4 8 16 32 64......(3 9 27 71..........................(4 16 24...(5 25 125..(6 36 36^2......(7 14 98 .....(8 64.. mxm.......det|(A-lambdasubi*I)tensorprod.(A-lambdasubj*I)..tensorprod(A-lambdasubk*I)|=0And now the fast sieve of Arostothenes.A in binary
Method to obtain prime numbers:det|A-lambdasubi*I|=0A=(1 111111111111111111..(2 4 8 16 32 64......(3 9 27 71..........................(4 16 24...(5 25 125..(6 36 36^2......(7 14 98 .....(8 64.. mxm.......det|(A-lambdasubi*I)tensorprod.(A-lambdasubj*I)..tensorprod(A-lambdasubk*I)|=0And now the fast sieve of Arostothenes.A in binary
A=(01 01 01 01 01 01 01 01 01 01 01 01...*(10 100 1000 10000 100000 1000000......
(11 111 (in decimal 27 81..........................*(100 10000 1000000...(101 (in decimal..25 125..((in decimal 6 36 36^2......((in decimal7 14 98 .....*(1000 1000000000.. mxmfor base=3*2=6 6 36 36^2 36^3=*(6|base3*2 10 100 1000 10000 100000 1000000......another interesting observation:pN/((pN)-1)->Dividendus=quotient*divisor+rest->pN=((pN)-1)*1+1P(N)-1/(P(N-1)-1=2^aP(N)-1/(P(N-1)-1=2^a due both are evenP(N)/P(N)-1/P(N-1)/P(N-1)-1==(P(N-1)-1)*P(N)/(P(N)-1)*P(N-1)=1=(1/2^a)*P(N)/(P(N)-1) =root(N for each N->0 to inf)((1/2^a)*P(N)/(P(N)-1))-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------MOST INTUITIVE SOLUTION-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
because det(L) = 1; the right hand side is easily computed as the product of all diagonal elements of U multiplied with the determinant of the permutation matrix P (which is +1 for an even permutation and is -1 for an odd permutation). This is more efficient than calculating the determinant of A because the determinant of a (upper or lower) triangular matrix is the product of its diagonal elements.
A small example:
Therefore
due the calculations are linnear
det(A-lambdasubi*I=C)=0->in a base B we obtain the diagonal matrix ,
B*C*B^-1=I
(2 0 0 0.................................0) ( )=(-(2^n)-1 n=0
(0 4 0 0..................................0) ---- (-2^n)-2=0
(----------------------------...............0) ... ...
C=((0 0 2^(a-1) 00..,00.....................0) X= (2^(n-1)-(2^n))=0=-1/2=lambdaN for all n
(0 0 3 0 0 --...............0)
( ----------------------------------------
(0 0 0 3^4 0 ....................0)
(0 0 0 0 0 3^b 0..0..00)
( ........................................ )
(0...... ...pi^k................0)
. (..................................................0)
(0....----------..........................pn^n) , det(C)=p(n+1)-1 even,pair number=2^a*3^b*5^c*pn^n ,
it conforms the system of equations: det(C-2^a*I)=0..det(C-3^b*I)=0
we also can use the conjecture of coldbach pi+pm=((p(n+1)-1))*(1/(p(n+1)-1)^n)=even
(1/(p(n+1)-1)^n)*(pi+pm)=((p(n+1)-1))->(1/(p(n+1)-1)^n)*(2^a*3^b*5^c*p(i-1)^(i-1)+2^a*3^b*5^c*p(m-1)^(m-1))
q,c,d
seeing at another perspective
(1 0 0 ) (0 0 1)
C=(2 0 0...) C-1=(0 0 1/2)
(0 4 0...) (0 1/4 0)
(0 0 8...) (1/8 0 0)
(......... ) ............
(0 0 0 2^a) (1/2^a 0 0)
Det[(C)tensor product x Ntimes x C x (D) .. Ntimes D x ... N x Ntimes x..xN]
= ((lambda1=-1=(1/(2*2^2*2^4*2^3*..2^N)^(2*2^2*2^4*2^3*..2^N))+1)*(lambda2=
-1=1/(3^2*3^3*3^4*..*3^N)^ (3^2*3^3*3^4*..*3^N))+1)*...*(lambdaN=
-1=1/(pN*pN^2*pN^3*..*P^N)^(pN*pN^2*pN^3*..*P^N))+1)=zeta(S)=0
=((p^S)-1)/p^S=
Det(C-1)*Det[(C-1)tensor product x (D-1)x..x(N-1)]*Det(1/C^t (tensor product=x) 1/D^t ) x 1/E^t x..1/(N-1)^t)*
Det(CxDx..xN)*(C^-1xD^-1x..xN^-1)=Ix..Ntimes..xI lambdai=1^N just need to apply in a recurrent form conjecture of coldback prime1+prime2=even so we also can use the conjecture of coldbach pi+pm=((p(n+1)-1))*(1/(p(n+1)-1)^n)=even develop and obtain final soilution
Relation to the Riemann zeta function
Some derivatives of fractional harmonic numbers are given by:
And using Maclaurin series, we have for x<1 :
where ζ(n) is the Riemann zeta function.
C=(C/2-2*lambda*IxIxI..I) ->lambdasubi=2^i
D=(3 0 0...)
(0 9 0...)
(0 0 27..)
.....
(0 0 0 3^b)
D=D/3-3lambdaIxIxI..I .>lambdasubj=3^j
E=(5 0 0...0)
(0 0 25..0)
...........
(0 0 0 5^c)
....
N=(pn 0 0 ..0)
(0 pn^2 0..0)
. ................
(0 0 0 pn^z)
|((C tensor product D tensor product E ... tensor product N)-(lambda=(2^a*3^b*5^c*p(i-1)^(i-1) ( I tensor product I ... tensor product I) ....|=0->lambdasubi=pi=
PA=LU->PA=I*B
B*C=I*B->C=B^-1*B=B^t*B/det|B|->det(C) normalized= p(n+1)-1=(2^a/(2^a*3^b*5^c*pn^n))*(3^b/(2^a*3^b*5^c*pn^n))*..*((pn^n/(2^a*3^b*5^c*pn^n))=
(p(n+1)-1)=((p(n+1)-1))*(1/(p(n+1)-1)^n)
det(A-lambdasubi*I=C)=0
Method to obtain prime numbers:
det|A'-lambdasubi*I|=0
det |M'|<>0,M' = operaciones lineales quitando los dependientes con A'
A'=(1 111111111111111111..
(2 4 8 16 32 64......
(3 9 27 71..........................
(4 16 24...
(5 25 125..
(6 36 36^2......
(7 14 98 .....
(8 64.. mxm
....
A=(1 0 0 0 0 0 00 0 0 0 0..
(2 4 0 0 0 0 00 0 0 0 ......
(3 9 27 0 0 0 0 0 0 0 0..........................
(4 16 32 64 0 0 0 00 0...
(5 25 125 625 5^6 0 0 0..
(6 36 36^2 36^4 36^5 36^6 36^7......
( ....................................... mxm
det|A-lambdasubi*I|=0
hacemos combinaciones lineales de las filas que nos da la misma det de la matriz
M'=(
(fila1=(pot2)A0,0..n+A1,0..n+A3,0..n+A7,0..n+A(8+64-1),0..n...
(fila2(pot3)A0,0..n+A2,0..n+A8,0..n+A16,0..n+A24,0..n+......
(fila3=(pot5).A0,0..n+A4,0..n..
tenemos que , we have that
fila1=2^m=Am,0=pow(2m)(A0,0),A7,0=pow(2)(A3,0);A3,0=pow(2)(A1,0=2*A0,0))
fila2=3^m=Am,0=pow(3m)(A0,0),A8,0=pow(3)(A4,0);A3,0=pow(3)(A2,0=3*A0,0))
fila3=5^m=Am,0=pow(5m)(A0,0),A100,0=pow(5)(A20,0);A20,0=pow(3)(A4,0=3*A0,0))
luego then
fila1=2^m=Am,0;xm*pow(2m)(A0,0)+..+x2*A7,0+x1*pow(2)(A3,0);A3,0+x0*pow(2)(A1,0=2*A0,0))=0
fila2=3^m=Am,0;xm*pow(3m)(A0,0)+..+x2*A8,0+x1*pow(3)(A4,0);A3,0+x0*pow(3)(A2,0=3*A0,0))=0
fila3=5^m=Am,0;xm*pow(5m)(A0,0)+..+x2*A100,0+x1*pow(5)(A20,0);A20,0+x0*pow(5)(A4,0=3*A0,0))=0
luego then
det|fila1=2^m=(Am,0)pow(2m)-lambdam.. ,,A7,0 ...pow(2)(A3,0);A3,0.... ... pow(2)(A1,0=2*A0,0))=0
|fila2=3^m=Am,0;pow(3m)(A0,0).......x2*A8,0;pow(3)(A4,0)-lambda1;A3,0*pow(3)(A2,0=3*A0,0))=0
|fila3=5^m=Am,0;xm*pow(5m)(A0,0)+..+x2*A100,0+x1*pow(5)(A20,0);A20,0+pow(5)(A4,0=3*A0,0))-lambda0=0
(1-lamdba1)*(2-lambda2)*(3-lambda3)*..*(p-lambdap)=0
(1-lamdba1)^-S*(2-lambda2)^-S*(3-lambda3)^-S*..*(p-lambdap)^-S=0^-S=0
that is the case the matrix M' has 2 rows repeated -S/2=a, -S/3=b,.. integer that gives out trivial zeroes
for det(A)=0-> prod(Ai,i)*...*((Ai-m,i-m)^-S=Aii^(-m*S)) S=-2,-3,-5,-7..prime gives out trivial zeroes
so probe the hipothesis of riemman results trivial:
((Ai-m,i-m)^-S=Aii^(m/2)) that is the definition of the trigonal matrix S=-1/2 S=-1/2+ib not altering the condition of det(A)=0
prod(Ai,i)*...*((Ai-m,i-m)^-S=Aii^(-m*S))thats it the polynomia
- ab = ebloga
0=(number-lambda)^-S=number^m-lambda^-mS'Ai+i=Ai+i,0 if(Ai-1,0=pi-1->A(i+i)-1,0->p(i+i-1)A=(1 0 0 0(2 4 0 0(3 9 27 0(4 16 32 64 0The simplest method of computing an requires n−1 multiplication operations, but it can be computed more efficiently as illustrated by the following example. To compute 2100, note that 100 = 64 + 32 + 4. Compute the following in order:
- 22 = 4
- (22)2 = 24 = 16
- (24)2 = 28 = 256
- (28)2 = 216 = 65,536
- (216)2 = 232 = 4,294,967,296
- (232)2 = 264 = 18,446,744,073,709,551,616
- 264 232 24 = 2100 = 1,267,650,600,228,229,401,496,703,205,376
This series of steps only requires 8 multiplication operations instead of 99 (since the last product above takes 2 multiplications).

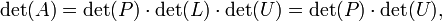
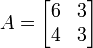

![\frac{d^n H_x}{dx^n} = (-1)^{n+1}n!\left[\zeta(n+1)-H_{x,n+1}\right]](http://upload.wikimedia.org/math/c/e/1/ce1d807f8f4d1a1f49179fca8e3d40d8.png)
![\frac{d^n H_{x,2}}{dx^n} = (-1)^{n+1}(n+1)!\left[\zeta(n+2)-H_{x,n+2}\right]](http://upload.wikimedia.org/math/0/d/2/0d266ed99ba76f4dce810d9b22a0329c.png)
![\frac{d^n H_{x,3}}{dx^n} = (-1)^{n+1}\frac{1}{2}(n+2)!\left[\zeta(n+3)-H_{x,n+3}\right]](http://upload.wikimedia.org/math/b/3/f/b3f36dd03c83a83081e622c54b4e3395.png)



No hay comentarios:
Publicar un comentario
Ayudenos a mejorar el blog con su opinion...