Its not im clever than anybody because i am the most talking about intelligence , normal person in the world , and what appears in continuation is the conclusion of a very complicated work develeoped firstly by the 2001 Nobel Prize laureate Wolfwang Ketterle, consider what follows in continuation just a suggestion to reach with a limit of the precision of pointing the beams of laser atoms developed by Mr ketterle a method to reach temperatures very close to absolute
using Abvaromov-
Good Morning r Professor, using Abaromov-Bohm Effect pushing laser 3d ions so they make a 3d grid the result of magnetical forces appeared will make spin the bose einstein condensate so it can make the desred oscilalation or just make a quite unmoved quantum ball.Best regards David.
Aharonov–Bohm effect From Wikipedia, the free encyclopedia
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–
using Abvaromov-
Good Morning r Professor, using Abaromov-Bohm Effect pushing laser 3d ions so they make a 3d grid the result of magnetical forces appeared will make spin the bose einstein condensate so it can make the desred oscilalation or just make a quite unmoved quantum ball.Best regards David.
Aharonov–Bohm effect From Wikipedia, the free encyclopedia
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–
Werner Ehrenberg and Raymond E. Siday first predicted the effect in 1949,[2] and similar effects were later rediscovered by Yakir Aharonov and David Bohm in 1959.[3] After publication of the 1959 paper, Bohm was informed of Ehrenberg and Siday's work, which was acknowledged and credited in Bohm and Aharanov's subsequent 1961 paper.[4][5] A general review can be found in Peshkin and Tonomura (1989).[6]
Contents[hide] |
[edit]Significance
The Aharonov–Bohm effect is important conceptually because it illustrates the physicality of electromagnetic potentials, Φ and A, whereas previously it was possible to argue that only the electromagnetic fields, E and B, were physical and that the electromagnetic potentials, Φ and A, were purely mathematical constructs (being non-unique, in addition to not appearing in the Lorentz Force formula). The non-uniqueness of the electromagnetic potentials is a manifestation of electromagnetic gauge freedom, with the electric and magnetic fields and forces being gauge invariant and therefore directly observable (the fields do appear in the Lorentz force formula).
Similarly, the Aharonov-Bohm effect illustrates that the Lagrangian approach to dynamics, based on energies, is not just a computational aid to the Newtonian approach, based on forces. Thus the Aharonov–Bohm effect validates the view that forces are an incomplete way to formulate physics, and potential energies must be used instead. In fact Richard Feynman complained[citation needed] that he had been taught electromagnetism from the perspective of E and B, and he wished later in life he had been taught to think in terms of the A field instead, as this would be more fundamental. In Feynman's path-integral view of dynamics, the A field directly changes the phase of an electron wave function, and it is these changes in phase that lead to measurable quantities.
The Aharonov–Bohm effect shows that the local E and B fields do not contain full information about the electromagnetic field, and the electromagnetic four-potential, A, must be used instead. By Stokes' theorem, the magnitude of the Aharonov–Bohm effect can be calculated using A alone, or using E plus B alone. But when using the fields, the effect depends on the field values in a region from which the test particle is excluded, not only classically but also quantum mechanically. In contrast, the effect depends on A only in the region where the test particle is allowed. Therefore we can either abandon the principle of locality (which most physicists are reluctant to do) or we are forced to accept the realisation that the electromagnetic 4-potential - composed of Φ and A - offers a more complete description of electromagnetism than the electric and magnetic fields can. In classical electromagnetism the two descriptions were equivalent. With the addition of quantum theory, though, the electromagnetic potentials Φ and A are seen as being more fundamental. [7] The E and B
This effect was chosen by the New Scientist magazine as one of the "seven wonders of quantum world".[8]
[edit]Magnetic solenoid effect
The magnetic Aharonov–Bohm effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choice for the electromagnetic potential, of which the magnetic vector potential A forms part.
Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field B, but non-zero A (by  ), acquires a phase shift
), acquires a phase shift  , given in SI units by
, given in SI units by
 ), acquires a phase shift
), acquires a phase shift  , given in SI units by
, given in SI units by
Therefore particles, with the same start and end points, but travelling along two different routes will acquire a phase difference Δφ determined by the magnetic flux ΦB through the area between the paths (via Stokes' theorem and 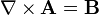 ), and given by:
), and given by:
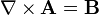 ), and given by:
), and given by:
In quantum mechanics the same particle can travel between two points by a variety of paths. Therefore this phase difference can be observed by placing a solenoid between the slits of a double-slit experiment (or equivalent). An ideal solenoid encloses a magnetic field B, but does not produce any magnetic field outside of its cylinder, and thus the charged particle (e.g. an electron) passing outside experiences no magnetic field B. However, there is a (curl-free) vector potential A outside the solenoid with an enclosed flux, and so the relative phase of particles passing through one slit or the other is altered by whether the solenoid current is turned on or off. This corresponds to an observable shift of the interference fringes on the observation plane.
The same phase effect is responsible for the quantized-flux requirement in superconducting loops. This quantization occurs because the superconducting wave function must be single valued: its phase difference Δφ around a closed loop must be an integer multiple of 2π (with the charge for the electron Cooper pairs), and thus the flux Φ must be a multiple of h/2e. The superconducting flux quantum was actually predicted prior to Aharonov and Bohm, by F. London in 1948 using a phenomenological model.[9]
The magnetic Aharonov–Bohm effect was experimentally confirmed by Osakabe et al. (1986),[10] following much earlier work summarized in Olariu and Popèscu (1984).[11] Its scope and application continues to expand. Webb et al. (1985)[12] demonstrated Aharonov–Bohm oscillations in ordinary, non-superconducting metallic rings; for a discussion, see Schwarzschild (1986)[13] and Imry & Webb (1989).[14]Bachtold et al. (1999)[15] detected the effect in carbon nanotubes; for a discussion, see Kong et al. (2004).[16]
[edit]Monopoles and Dirac strings
The magnetic Aharonov–Bohm effect is also closely related to Dirac's argument that the existence of a magnetic monopole can be accommodated by the existing magnetic source-free Maxwell's equations if both electric and magnetic charges are quantized.
A magnetic monopole implies a mathematical singularity in the vector potential, which can be expressed as an Dirac string of infinitesimal diameter that contains the equivalent of all of the 4πg flux from a monopole "charge" g. The Dirac string starts from, and terminates on, a magnetic monopole. Thus, assuming the absence of an infinite-range scattering effect by this arbitrary choice of singularity, the requirement of single-valued wave functions (as above) necessitates charge-quantization. That is,  must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
 must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
Like the electromagnetic potential A the Dirac string is not gauge invariant (it moves around with fixed endpoints under a gauge transformation) is also not directly measurable.
[edit]Electric effect
Just as the phase of the wave function depends upon the magnetic vector potential, it also depends upon the scalar electric potential. By constructing a situation in which the electrostatic potential varies for two paths of a particle, through regions of zero electric field, an observable Aharonov–Bohm interference phenomenon from the phase shift has been predicted; again, the absence of an electric field means that, classically, there would be no effect.
From the Schrödinger equation, the phase of an eigenfunction with energy E goes as 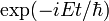 . The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
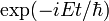 . The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
where t is the time spent in the potential.
The initial theoretical proposal for this effect suggested an experiment where charges pass through conducting cylinders along two paths, which shield the particles from external electric fields in the regions where they travel, but still allow a varying potential to be applied by charging the cylinders. This proved difficult to realize, however. Instead, a different experiment was proposed involving a ring geometry interrupted by tunnel barriers, with a bias voltage V relating the potentials of the two halves of the ring. This situation results in an Aharonov–Bohm phase shift as above, and was observed experimentally in 1998.[17]
[edit]Aharonov–Bohm nano rings
Nano rings were created by accident[18] while intending to make quantum dots. They have interesting optical properties associated with excitons and the Aharonov–Bohm effect.[18] Application of these rings used as light capacitors or buffers includesphotonic computing and communications technology. Analysis and measurement of geometric phases in mesoscopic rings is ongoing.[19][20][21]
[edit]Mathematical interpretation
| This section needs additional citations for verif Please help improve this article by adding reliable references. Unsourced material may be challenged and removed. ( |
In the terms of modern differential geometry, the Aharonov–Bohm effect can be understood to be the monodromy of a flat complex line bundle. The U(1)-connection on this line bundle is given by the electromagnetic four-potential A as  where d
where d  . The curvature form of the connection,
. The curvature form of the connection, 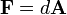 , is the electromagnetic field strength, where
, is the electromagnetic field strength, where  is the 1-form corresponding to the four-potential. The holonomy of the connection,
is the 1-form corresponding to the four-potential. The holonomy of the connection,  around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is
around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is  ; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
 where d
where d  . The curvature form of the connection,
. The curvature form of the connection, 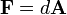 , is the electromagnetic field strength, where
, is the electromagnetic field strength, where  is the 1-form corresponding to the four-potential. The holonomy of the connection,
is the 1-form corresponding to the four-potential. The holonomy of the connection,  around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is
around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is  ; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
In any simply connected region outside of the tube we can find a gauge transformation (acting on wave functions and connections) that gauges away the vector potential. However, if the monodromy is non trivial, there is no such gauge transformation for the whole outside region. If we want to ignore the physics inside the conductor and only describe the physics in the outside region, it becomes natural to mathematically describe the quantum electron by a section in a complex line bundle with an "external" connection  rather than an external EM field
rather than an external EM field 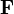 (by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
(by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
 rather than an external EM field
rather than an external EM field 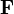 (by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
(by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
Effects with similar mathematical interpretation can be found in other fields. For example, in classical statistical physics, quantization of a molecular motor motion in a stochastic environment can be interpreted as an Aharonov–Bohm effect induced by a gauge field acting in the space of control parameters.[22]
[edit]See also
[edit]References
- ^ Sjöqvist, E (2002). "Locality and topology in the molecular Aharonov-Bohm effect". Physical Review Letters 89 (21): 210401. doi:10.1103/
PhysRevLett.89.210401.arXiv:qu ant-ph/0112136. - ^ Ehrenberg, W; Siday, RE (1949). "The Refractive Index in Electron Optics and the Principles of Dynamics".Proceedings of the Physical Society B 62: 8–21.doi:10.1088/0370-1301/62/
1/303. - ^ Aharonov, Y; Bohm, D (1959). "Significance of electromagnetic potentials in quantum theory". Physical Review 115: 485–491. doi:10.1103/PhysRev.
115.485. - ^ Peat, FD (1997). Infinite Potential: The Life and Times of David Bohm.
...
[Mensaje recortado] Ver todo el mensaje
 Responder Responder |  Reenviar Reenviar |
- Mostrar texto citado -
Aharonov–Bohm effect
- Mostrar texto citado -
- Mostrar texto citado -- ^ Peat, FD (1997). Infinite Potential: The Life and Times of David Bohm. Addison-Wesley. ISBN 0-
201-40635-7. - ^ Aharonov, Y; Bohm, D (1961). "Further Considerations on Electromagnetic Potentials in the Quantum Theory".Physical Review 123: 1511–1524.doi:10.1103/PhysRev.
123.1511. - ^ Peshkin, M; Tonomura, A (1989). The Aharonov-Bohm effect. Springer-Verlag. ISBN
3-540-51567-4. - ^ Feynman, R. The Feynman Lectures on Physics. 2. p. 15-5. "knowledge of the classical electromagnetic field acting locally on a particle is not sufficient to predict its quantum-mechanical behavior. and ...is the vector potential a "real" field? ... a real field is a mathematical device for avoiding the idea of action at a distance. .... for a long time it was believed that A was not a "real" field. .... there are phenomena involving quantum mechanics which show that in fact A is a "real" field in the sense that we have defined it..... E and B are slowly disappearing from the modern expression of physical laws; they are being replaced by A[the vector potential] and
[the scalar potential]"
- ^ "Seven wonders of the quantum world", newscientist.com
- ^ London, F (1948). "On the Problem of the Molecular Theory of Superconductivity". Physical Review 74: 562.doi:10.1103/PhysRev.74.562
. - ^ Osakabe, N; et al. (1986). "Experimental confirmation of Aharonov-Bohm effect using a toroidal magnetic field confined by a superconductor". Physical Review A 34: 815.doi:10.1103/PhysRevA.34.
815. - ^ Olariu, S; Popescu, II (1985). "The quantum effects of electromagnetic fluxes". Reviews of Modern Physics 57: 339. doi:10.1103/RevModPhys.
57.339. - ^ Webb, RA; Washburn, S; Umbach, CP; Laibowitz, RB (1985). "Observation of h/e Aharonov-Bohm Oscillations in Normal-Metal Rings". Physical Review Letters 54: 2696.doi:10.1103/PhysRevLett.
54.2696. - ^ Schwarzschild, B (1986). "Currents in Normal-Metal Rings Exhibit Aharonov–Bohm Effect". Physics Today 39(1): 17. doi:10.1063/1.2814843.
- ^ Imry, Y; Webb, RA (1989). "Quantum Interference and the Aharonov-Bohm Effect". Scientific American 260 (4).
- ^ Schönenberger, C; Bachtold, Adrian; Strunk, Christoph; Salvetat, Jean-Paul; Bonard, Jean-Marc; Forró, Laszló; Nussbaumer, Thomas (1999). "Aharonov–Bohm oscillations in carbon nanotubes". Nature 397: 673.doi:10.1038/17755.
- ^ Kong, J; Kouwenhoven, L; Dekker, C (2004). "Quantum change for nanotubes". Physics World. Retrieved 2009-08-17.
- ^ van Oudenaarden, A; Devoret, Michel H.; Nazarov, Yu. V.; Mooij, J. E. (1998). "Magneto-electric Aharonov–Bohm effect in metal rings". Nature 391: 768.doi:10.1038/35808.
- ^ a b Fischer, AM (2009). "Quantum doughnuts slow and freeze light at will". Innovation Reports. Retrieved 2008-08-17.
- ^ Borunda, MF; et al. (2008). "Aharonov-Casher and spin Hall effects in two-dimensional mesoscopic ring structures with strong spin-orbit interaction". arΧiv:0809.0880
[cond-mat.mes-hall]. - ^ Grbic, B; et al. (2008). "Aharonov-Bohm oscillations in p-type GaAs quantum rings". Physica E 40: 1273.doi:10.1016/j.physe.2007.
08.129. arXiv:0711.0489. - ^ Fischer, AM; et al. (2009). "Exciton Storage in a Nanoscale Aharonov-Bohm Ring with Electric Field Tuning". Physical Review Letters 102: 096405.doi:10.1103/
PhysRevLett.102.096405.
[Mensaje recortado] Ver todo el mensaje
 Responder Responder |  Reenviar Reenviar |
mostrar detalles 17:56 (hace 9 horas)
|
Good afternoon Mr Professor exactly the lasers cut the bose- einstein condensate leaving a 3d dice , if you resend the lasers through the holes now with an accelerated ions with a very small phase difference there is a probability that the beam passes over the closest hole also creating the A.-bohm effect making suddenly move appart the rests of the BEC that phase define a dice oscillation if you make the same at the same time with entanglement accelerated ions set with an opposite resend phase you will have two dices BEC oscillating in oppositiveness yous beam with the atom laser at the same time one BEC dice pulse atom to another. this is the smallest temperature get method procedure i can imagine to ever set by EM methods-
----------------------------------------------------------------------------------------------------------------------------------------------------------------------
the Asyntotically problem of xoring to obtain qc qubit orthogonality
In fact i didnt realize until just now but with A.-Bohm effect and a double split orthogonal sided boxes with ions inside it
can be reached orthogonality if we split the electron or ion with a ghost multiple divided beam for each box at enogh speed
solving the problem of reaching asyntotically orthogonality reaching at the same time instead of using a qc xor operator,
for a big number of quantum computer made qubits
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
The perfect GPS:just consider this as one more of my stravagances in physics
The idea is simply we have an satelllite orbiting at a stationary orbit at Van Allen Belts,later i will explain why this
then we have our car double split experiment sender that pass trough a hole in the front foot of the car the other hole in the back roof of the car then we have a detector of a pair of electromagnetic waves signals
that are in entangled stte if we do pass two beams for later entangled then you fave both graphs eb1 and eb2.
phi(A)+phi(B)=phi(A')+phi(B`)
due quantum mechanics both pass at the same time at detector C in the satellite even when AB distance = 1 meter and AC>BC but if both rays provide for a single one the whole energy should conserve
so mass eb2
so we can calculate distance precisly in base T in base diference of masses with an antimateria consumed measured result the coliding of eb1 and eb2
H=T-Uso all params are knew., it also can be mesaured experimentally with the solar panel increase of current easure due anhilation of matter,alsoi can consider ions instead of electrons for sending wave position data
Cinturones de Van Allen
Los cinturones de Van Allen son ciertas zonas de la magnetosfera terrestre donde se concentran las partículas cargadas. Son llamados así en honor de su descubridor James Van Allen. Fueron descubiertos gracias al lanzamiento del satélite estadounidense Explorer 1, el cual fue en principio un fracaso debido a su forma alargada que junto con un sistema de control mal diseñado "descontroló" este dentro de su orbita. En la imagen podemos ver el Explorer 1 atravesando dichos cinturones.
Estos cinturones son áreas en forma de anillo de superficie toroidal en las que gran cantidad de protones y electrones se están moviendo en espiral entre los polos magnéticos del planeta, y se estructura en dos cinturones: uno interior y otro exterior. El cinturón interior está a unos 1.000 km por encima de la superficie de la Tierra y se extiende por encima de los 5.000 km (los satélites de orbita baja (LEO) interesan que estén a una altitud considerable para evitar que la resistencia residual atmosférica reduzca el tiempo de vida de este, pero a la vez deben estar por debajo de los 1000 km para no entrar en cinturones de radiación, muy perjudiciales para dichos satélites); por su parte, el cinturón exterior se extiende desde aproximadamente 15.000 km hasta los 20.000 km. Este cinturón exterior en concreto, no afecta a satélites de orbitas altas/medias (MEO) como pueden ser los Geoestacionarios (GEO) situados en torno a 35000km de altitud.
Una región del cinturón interior, conocida como Anomalía del Atlántico Sur (SAA) se extiende a orbitas bajas y es peligroso para las naves y satélites artificiales que lo atraviesen, pues tanto los equipos electrónicos como los seres humanos pueden verse perjudicados por la radiación.
Estos cinturones de radiación se originan debido al intenso campo magnético de la tierra, originado por la rotación de esta, que atrapa las partículas cargadas (plasma) proveniente del sol (viento solar) de acuerdo a las leyes de la magnetohidrodinamica
[editar]Véase también
[editar]Enlaces externos
Producción y costo de la antimateria
La antimateria es la sustancia más cara del mundo, con un costo estimado de unos 60.000 millones de USD el miligramo.8 9 La producción de antimateria, además de consumir enormes cantidades de energía, es muy poco eficiente, al igual que la capacidad de almacenamiento, que ronda sólo el 1% de las partículas creadas. Además, debido a que la antimateria se aniquila al contacto con la materia, las condiciones de almacenamiento —confinamiento mediante campos electromagnéticos—, tienen igualmente un costo elevado.
Otra estimación de su costo la dio el CERN, cuando dijo que había costado algunos cientos de millones de francos suizos la producción de una milmillonésima de gramo.10
Debido a esto, algunos estudios de la NASA plantean recolectar mediante campos magnéticos la antimateria que se genera de forma natural en los Cinturones de Van Allen de la Tierra, o incluso en los cinturones de los grandes planetas gaseosos comoJúpiter.11
También se trabaja en mejorar la tecnología de almacenaje de antimateria. El Dr. Masaki Hori ha anunciado un método de confinamiento de antiprotones por radiofrecuencia, lo que según sus palabras podría reducir el contenedor al tamaño de una papelera.12
En noviembre de 2008 la doctora Hui Chen, del Lawrence Livermore National Laboratory de Estados Unidos, anunció que ella y su equipo habrían creado positrones al hacer incidir un breve, aunque intenso, pulso láser a través de una lámina de oro blanco de pocos milímetros de espesor, esto habría ionizado al material y acelerado sus electrones. Los electrones acelerados emitieron cuantos de energía, que al decaer dieron lugar a partículas materiales, dando también como resultado positrones.13
Equivalencia entre masa y energía
La equivalencia entre la masa y la energía dada por la expresión de la teoría de la relatividad de Einstein,
indica que la masa conlleva una cierta cantidad de energía aunque se encuentre en reposo, concepto ausente en mecánica clásica.
La ecuación de extender la ley de conservación de la energía a fenómenos como la desintegración radiactiva. La fórmula establece la relación de proporcionalidad directa entre la energía E (según la definición hamiltoniana) y la masa m, siendo la velocidad de la luz c elevada al cuadrado la constante de dicha proporcionalidad.
También indica la relación cuantitativa entre masa y energía en cualquier proceso en que una se transforma en la otra, como en una explosión nuclear. Entonces, E puede tomarse como la energía liberada cuando una cierta cantidad de masa m es desintegrada, o como la energía absorbida para crear esa misma cantidad de masa. En ambos casos, la energía (liberada o absorbida) es igual a la masa (destruida o creada) multiplicada por el cuadrado de la velocidad de la luz.
- Energía en reposo = Masa × (Velocidad de la luz)2
Contenido[ocultar] |
[editar]Interpretación geométrica espacio-temporal de la ecuación
La Relatividad, esencialmente, pretende explicar el curso de los procesos naturales a través de la geometría del espacio-tiempo, la cual impone una serie de restricciones que determinan el desarrollo de tales procesos. La geometría del espacio-tiempo no es la euclídea habitual (no se cumple el teorema de Pitágoras, por decirlo así), sino que es la geometría de Minkowski, cuyas reglas son diferentes. Las magnitudes físicas interesantes en Relatividad son las que poseen cuatro componentes, porque sabemos que el espacio-tiempo relativista tiene también cuatro dimensiones (tres espaciales y una temporal).
temporales de un sistema de referencia cualquiera ligado a un observador. Las tres proyecciones de este vector 4-ímpetu sobre los ejes espaciales -hablando libremente- serían lo que clásicamente (en la mecánica de Newton) llamamos las tres componentes del impulso (o momento lineal).
Por otro lado, la proyección del vector 4-ímpetu sobre el eje del tiempo nos daría la masa-energía relativa (aquella que mide un observador que no está en reposo con respecto al objeto al cual asociamos ese vector 4-ímpetu). El módulo del vector 4-ímpetu (su "longitud" en el dibujo) se calcula mediante la regla que ponía en el anterior mensaje, y eso es la masa-energía propia (la que mediría un observador en reposo con respecto al objeto). Cuando ese objeto es un fotón no podemos medir directamente la masa-energía propia, solo calcularla, y resulta que siempre es cero (es una propiedad peculiar de los fotones). Pero no importa porque nosotros sólo podemos manejar con sentido físico medible la masa-energía relativa y las componentes del impulso.
[editar]Aplicaciones de la ecuación
La ecuación, E=mc2, válida en el contexto de la relatividad especial, se aplica a todos los objetos dentro un espacio-tiempo plano (o asintóticamente plano).
Cuando la ecuación se aplica a un objeto que no se encuentra en movimiento (lo cual significa que el objeto está siendo visto desde un punto de referencia en el cual el objeto se encuentra en reposo), tenemos la expresión E=mc2, en el cual E y m son la energía y masa "propias" (gráficamente igual a la longitud del 4-vector antes mencionado). Por la identidad masa-energía, haciendo la velocidad de la luz igual a la unidad, tenemos E = m. Este mismo objeto podría encontrarse en movimiento desde otro marco de referencia, y para este sistema tendríamos una masa-energía relativa y además tres componentes del impulso.
Cabe notar que en la física moderna la masa y la energía pueden considerarse idénticas. Cualquier ecuación en la cual aparezcan dos magnitudes ligadas por una constante universal, puede interpretarse legítimamente como la identidad entre dichas magnitudes, ya que la constante universal puede igualarse a la unidad por un cambio de unidades. Esto es especialmente claro en el caso de la Relatividad.
[editar]Utilizando la masa relativista
En los ensayos de Einstein (uno de los cuales se puede encontrar en esta página) la variable m representaba lo que ahora conocemos como masa relativista. Dicha masa se relaciona a la masa estacionaria, que es la masa de un objeto que se encuentra fijo desde el marco de referencia siendo utilizado. La masa relativista de un objeto cambia con la velocidad de un objeto, se incrementa a medida que la velocidad de un objeto incrementa desde el punto de vista utilizado, mientras que la masa estacionaria es una cantidad fija. Las dos masas se relacionan entre sí según la ecuación:
Para obtener la ecuación de E = mc2 se debe de modificar la ecuación E2 = p2c2 + m2c4 asignándole un valor de cero a p (p = 0) lo que significa que v también tiene que ser igual a cero (v = 0). Según se puede observar, el objeto esta fijo (su velocidad es de cero) y E2 es igual a m2c4, o sea E = mc2. E = mc2 solo se aplica en este caso en particular, en el cual la masa no está en movimiento. Si la masa se encuentra en movimiento es necesario volver a insertar la multiplicación del cuadrado de las variables p y c en la ecuación (p2c2).
Si se le asigna un valor de cero a la variable v (v = 0) en la ecuación  , se dice que la masa no se encuentra en movimiento, y como resultado la masa relativista y la masa estacionaria tienen el mismo valor. En este caso la ecuación E = mc2 puede escribirse como E = m0c2. No existe ninguna diferencia entre esta ecuación y E = mc2 con excepción, quizás, de que se podría decir que m0 representa a v = 0.
, se dice que la masa no se encuentra en movimiento, y como resultado la masa relativista y la masa estacionaria tienen el mismo valor. En este caso la ecuación E = mc2 puede escribirse como E = m0c2. No existe ninguna diferencia entre esta ecuación y E = mc2 con excepción, quizás, de que se podría decir que m0 representa a v = 0.
 , se dice que la masa no se encuentra en movimiento, y como resultado la masa relativista y la masa estacionaria tienen el mismo valor. En este caso la ecuación E = mc2 puede escribirse como E = m0c2. No existe ninguna diferencia entre esta ecuación y E = mc2 con excepción, quizás, de que se podría decir que m0 representa a v = 0.
, se dice que la masa no se encuentra en movimiento, y como resultado la masa relativista y la masa estacionaria tienen el mismo valor. En este caso la ecuación E = mc2 puede escribirse como E = m0c2. No existe ninguna diferencia entre esta ecuación y E = mc2 con excepción, quizás, de que se podría decir que m0 representa a v = 0.
Si se usa la masa relativista de un objeto se tiene que cambiar la ecuación original a E = mc2 a E = m0c2 y esta no aplicaría a un objeto en movimiento ya que m0 solo se aplica al caso en el cual v = 0 y cuando v es igual a cero, m = m0.
[editar]Utilizando la masa en reposo
Los físicos modernos rara vez utilizan la masa relativista, razón por la cual m representa la masa en reposo y la variable E es la energía en reposo (la energía de un objeto que no se encuentra en movimiento) en la ecuación E = mc2. La ecuación que se utiliza para los objetos que se encuentran en movimiento es
En la ecuación p = γmv es el ímpetu del objeto. Esta ecuación se reduce a E = mc2 en los casos en que un objeto se encuentra en reposo. Por motivos de claridad la variable m representará la masa relativista y m0 representará la masa en reposo en el resto del artículo.
[editar]Aproximación de baja energía
Dado el hecho que la por que la energía en reposo es igual a m0c2, la energía total es igual a la suma de la energía cinética más la energía en reposo. La ecuación que genera el total de la energía cinética relativa es la siguiente:
A velocidades bajas esta ecuación debería de ser equivalente a la fórmula que se utiliza para obtener la energía cinética de un objeto:
.
Al expandir γ utilizando una serie de Taylor se puede demostrar que las dos ecuaciones concuerdan una con otra:
.
Si se inserta esta fórmula a la ecuación original se obtiene el siguiente resultado:
.
Como resultado se obtiene la expresión ½m0v2 = Energía total - Energía en reposo que también se puede reorganizar para que Energía total = Energía en reposo + ½m0v2. Esta ecuación genera un conflicto con la física de Newton en la cual toda la energía se consideraba como energía cinética. Esta nueva ecuación demostró que la relatividad era una corrección a la mecánica clásica y que en un ambiente de baja energía o en un régimen clásico la física relativa y la física de Newton no son equivalentes la una con la otra. Aunque la fórmula para obtener el total de energía no es igual, la ecuación para obtener solamente la energía cinética de un objeto sí es la misma.
Einstein demostró que la física clásica estaba errada cuando trataba de explicar objetos masivos u objetos que viajan a velocidades muy elevadas. En el caso de los objetos más pequeños y lentos, los cuales fueron la base de la física clásica de Newton, la física clásica si es compatible con la física moderna.
[editar]Ensayo de Einstein de 1905
La ecuación, E = mc2, no fue formulada exactamente en dicha forma en el ensayo de Albert Einstein publicado en 1905. Einstein tituló dicho ensayo "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" ("¿La inercia de un cuerpo depende de su contenido energético?", publicado en Annalen der Physik el 27 de septiembre). En la actualidad este ensayo se incluye en los ensayos de Einstein titulados colectivamente como los ensayos del annus mirabilis. La tesis del ensayo de 1905 fue: "Si un cuerpo genera energía, L, en la forma de radiación, su masa disminuye por L/c2." En este caso la radiación equivale a la energía cinética y el concepto de masa era el que en la física moderna equivale a la masa en reposo. La fórmula L/c2 equivale a la diferencia de masa antes y después de la expulsión de energía; esta ecuación no representa la masa total de un objeto. Cuando Einstein publicó su ensayo esta fórmula era una hipótesis y todavía no se había probado a través de experimentos.
[editar]Contribuciones de otros físicos
Einstein no fue el único físico en notar la relación de la energía y la masa pero sí en publicar esta relación como parte de una teoría mucho más importante, y si bien en deducir la relación de la energía con la masa desde otra teoría. Según Umberto Bartocci (historiador de matemáticas en la Universidad de Perugia), Olinto De Pretto, oriundo de Vicenza, Italia, ya había publicado la ecuación dos años antes que Einstein. Muchos historiadores no están de acuerdo con esta declaración o no le dan mucha importancia. Los que defienden a Einstein también sostienen que aún si fuese cierto que De Pretto fue el primero en publicar la fórmula, fue Einstein quien la pudo relacionar con la teoría de la relatividad.
[editar]Biografía
Se utilizó esta célebre ecuación (E=mc2) como el título de una biografía de Albert Einstein que se transmitió por televisión en el 2005. Dicho programa se enfocó principalmente en 1905.
[editar]Véase también
 Portal:Física. Contenido relacionado con Física.
Portal:Física. Contenido relacionado con Física.- Albert Einstein
- Celeritas la razón por la cual se utiliza la variable c en E=mc2.
- Relación de energía-momento
- Equivalencía masa-energía
- Masa relativista
- Teoría de la Relatividad Especial
- Inercia relativamente.
[editar]Fuentes
- Bodanis, David (2001). E=mc2: A Biography of the World's Most Famous Equation, Berkley Trade. ISBN 0-425-18164-2.
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.), W. H. Freeman. ISBN 0-7167-4345-0.
[editar]Enlaces externos
- Principio de Equivalencia entre Masa y Energía
- Ensayo de Albert Einstein de 1905 (inglés)
- Manuscrito de Einstein de 1912
- Astrocosmo.cl
- Información en web educacional quimicaweb.net
- Stanford Encyclopedia of Philosophy entry (En inglés)
- Espacio,tiempo,materia y vacío fisica.ru
- The Formula in Einstein's Equation
Unidades de Planck
Las unidades de Planck o unidades naturales son un sistema de unidades propuesto por primera vez en 1899 por Max Planck. El sistema mide varias de las magnitudes fundamentales del universo: tiempo, longitud, masa, carga eléctrica ytemperatura. El sistema se define haciendo que estas cinco constantes físicas universales de la tabla tomen el valor 1 cuando se expresen ecuaciones y cálculos en dicho sistema.
| Constante | Símbolo | Dimensión |
|---|---|---|
| velocidad de la luz en el vacío |  | L / T |
| Constante de gravitación | 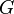 | L3/T2M |
| Constante reducida de Planck | 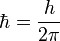 donde donde  es la constante de Planck es la constante de Planck | ML2/T |
| Constante de fuerza de Coulomb |  donde donde  es la permitividad en el vacío es la permitividad en el vacío | M L3/ Q2 T2 |
| Constante de Boltzmann |  | M L3/T2K |
El uso de este sistema de unidades trae consigo varias ventajas. La primera y más obvia es que simplifica mucho la estructura de las ecuaciones físicas porque elimina las constantes de proporcionalidad y hace que los resultados de las ecuaciones no dependan del valor de las constantes.
Por otra parte, se pueden comparar mucho más fácilmente las magnitudes de distintas unidades. Por ejemplo, dos protones se rechazan porque la repulsión electromagnética es mucho más fuerte que la atracción gravitatoria entre ellos. Esto se puede comprobar al ver que los protones tienen una carga aproximadamente igual a una unidad natural de carga, pero su masa es mucho menor que la unidad natural de masa.
También permite evitar bastantes problemas de redondeo, sobre todo en computación. Sin embargo, tienen el inconveniente de que al usarlas es más difícil percatarse de los errores dimensionales. Son populares en el área de investigación de larelatividad general y la gravedad cuántica.
Las unidades Planck suelen llamarse (en broma) por los físicos como las "unidades de Dios", porque elimina cualquier arbitrariedad antropocéntrica del sistema de unidades.
Contenido[ocultar] |
[editar]Expresión de leyes físicas en unidades Planck
-
- se convierte en
-
 utilizando unidades Planck.
utilizando unidades Planck.
-
- se convierte en
- La energía de una partícula o fotón con frecuencia radián
 en su función de onda
en su función de onda
-
- se convierte en
- La famosa ecuación de masa-energía de Einstein
-
- se convierte en
-
- (por ejemplo, un cuerpo con una masa de 5.000 unidades Planck de masa tiene una energía intrínseca de 5.000 unidades Planck de energía) y su forma completa
-
- se convierte en
-
- se convierte en
- La unidad de temperatura se define para que el promedio de energía térmica cinética por partícula por grado de libertad de movimiento
-
- se convierte en
-
- se convierte en
-
 .
.
-
- se convierten respectivamente en
-
- utilizando las unidades Planck. (Los factores
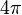 se pueden eliminar si
se pueden eliminar si 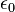 se hubiera normalizado, en vez de la constante de fuerza de Coulomb
se hubiera normalizado, en vez de la constante de fuerza de Coulomb  .)
.)
- utilizando las unidades Planck. (Los factores
[editar]Unidades de Planck básicas
Al dar valor 1 a las cinco constantes fundamentales, las unidades de tiempo, longitud, masa, carga y temperatura se definen así:
| Nombre | Dimensión | Expresión | Equivalencia aproximada en el Sistema Internacional |
|---|---|---|---|
| Tiempo de Planck | Tiempo (T) |  | 5.39121 × 10-44 s |
| Longitud de Planck | Longitud (L) |  | 1.61624 × 10-35 m |
| Masa de Planck | Masa (M) |  | 2.17645 × 10-8 kg |
| Carga de Planck | Carga eléctrica (Q) |  | 1.8755459 × 10-18 C |
| Temperatura de Planck | Temperatura (ML2T-2/k) |  | 1.41679 × 1032 K |
[editar]Unidades de Planck derivadas
Como en otros sistemas de unidades, las magnitudes físicas derivadas se pueden definir basándose en las Unidades de Planck.
| Nombre | Dimensión | Expresión | Equivalencia aproximada en el Sistema Internacional |
|---|---|---|---|
| Energía de Planck | Energía (ML2/T2) |  | 1.9561 × 109 J |
| Fuerza de Planck | Fuerza (ML/T2) | 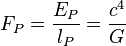 | 1.21027 × 1044 N |
| Potencia de Planck | Potencia (ML2/T3) |  | 3.62831 × 1052 W |
| Densidad de Planck | Densidad (M/L3) |  | 5.15500 × 1096 kg/m³ |
| Velocidad angular de Planck | Velocidad angular (1/T) | 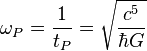 | 1.85487 × 1043 rad/s |
| Presión de Planck | Presión (M/LT2) | 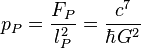 | 4.63309 × 10113 Pa |
| Intensidad eléctrica de Planck | Intensidad eléctrica (Q/T) |  | 3.4789 × 1025 A |
| Tensión eléctrica de Planck | Tensión eléctrica (ML2/T2Q) | 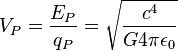 | 1.04295 × 1027 V |
| Resistencia eléctrica de Planck | Resistencia (ML2/T Q2) |  | 2.99792458 × 10¹ Ω |
VASIMR: Cómo llegar a Marte en 1 mes
Por: Kir Ortiz @ lunes, 27 de julio de 2009 Nota vista 10711 veces
Uno de los grandes inconvenientes que presenta el viaje a Marte es la enorme distancia que nos separa del planeta rojo. Las misiones tripuladas tardarían unos 6 meses en llegar, sin embargo, el nuevo motor iónico que están desarrollando en EEUU va a revolucionar los viajes espaciales hasta un punto sorprendente, pues se conseguirá llegar a Marte en apenas 39 días. La conquista roja la tenemos a la vuelta de la esquina.
La Luna está de moda, pero sólo a efectos recordatorios de la gran proeza del hombre al conseguir conquistarla. En realidad, Marte es el objetivo que atrae todas las miradas de los gobiernos más poderosos. Sin embargo, la distancia tan enorme que nos separa del planeta rojo llevaría unos 6 meses a una nave tripulada el conseguir su objetivo de aterrizar en la superficie. Esto significa muchos recursos económicos, muchas pruebas de simulación para ver como reaccionan los astronautas y muchas probabilidades de fracaso en la misión. Si hubiera alguna manera de reducir el tiempo de viaje, las posibilidades de emprender la conquista del planeta rojo ganarán muchos enteros.
Precisamente eso es lo que promete la empresa Ad Astra Rocket, que se fundó en 2005 por el físico de plasma y anterior astronauta de la lanzadera espacial Franklin Chang-Diaz. Están desarrollando un motor iónico que permitirá realizar el viaje a Marte en la increíble marca de 39 días. Hasta ahora, los motores empleados para lanzar misiones espaciales fundamentaban su funcionamiento en la quema de combustible químico para impulsar las naves fuera de la Tierra pero su potencia resultaba limitada para acelerar a velocidades necesarias para reducir el tiempo de viaje.
Aparecieron los motores iónicos, que aceleran los átomos eléctricamente cargados, o iones, a través de un campo eléctrico, impulsando de este modo la nave en la dirección opuesta y logrando la hazaña de seguir acelerando durante años a través del espacio hasta conseguirvelocidades de crucero muy elevadas. No tienen impulso inicial suficiente como para vencer la gravedad de la Tierra, pero una vez en el espacio son capaces de conseguir mayores velocidades que los motores químicos. Varias misiones espaciales ya han usado motores de iones, incluyendo la nave Dawn de la NASA, la cual está en ruta hacia los asteroides Vesta y Ceres, y la nave japonesa Hayabusa, que se encontró con el asteroide Itokawa en 2005. Sin embargo, el impulso alcanzado seguía siendo pequeño como para interesar a una posible misión a Marte.
Eso parece quedar resuelto con el nuevo modelo de motor iónico que están diseñando los de Ad Astra Rocket. Ha sido bautizado como VASIMR (Cohete de Magnetoplasma de Impulso Específico Variable) y tendrá un impulso mucho mayor que los anteriores gracias a que emplea de un generador de radiofrecuencias para calentar las partículas cargadas (plasma). El sistema funciona en dos fases. En una primera etapa, el motor funciona de manera similar a una máquina de vapor ya que el generador de radiofrecuencia calienta átomos de argón hasta que los electrones “hierven”, creando un plasma.
Por sí mismo, este plasma ya podría impulsar una nave pero el rendimiento conseguido resultaría poco eficiente así que los ingenieros de la compañía han agregado una segunda fase donde se calientan los iones aproximadamente a un millón de grados, una temperatura equiparable a la del centro del Sol. Eso lo puede hacer porque aprovecha el hecho de que en un potente campo magnético, los iones giran a una frecuencia fija. El generado de radiofrecuencia se ajusta a la misma frecuencia, inyectando energía extra a los iones. Los potentes campos magnéticos canalizan entonces el plasma fuera del motor, propulsando el cohete en la dirección opuesta.
Gracias al generador de radiofrecuencia, la potencia del VASIMR alcanza cientos de veces la de los motores iónicos que existen actualmente. “Es la fuente de plasma superconductora más potente jamás creada, por lo que sabemos”, dice Jared Squire, director de investigación de Ad Astra. Hasta el momento, los miembros del equipo han hecho funcionar el motor de dos etapas a una potencia de 50 kW. Esperan alcanzar los 200 kW de potencia en las pruebas que realizarán dentro de unos días, que será suficiente para proporcionar aproximadamente medio kilo de empuje. Eso puede sonar miserable, pero hay que tener en cuenta que en el espacio puede propulsar dos toneladas de carga.
Con los niveles de potencia actuales, VASIMR podría servir como remolcador espacial, para llevar satélites a sus órbitas, lanzar cargas a bases lunares e, incluso, conseguiría alcanzarasteroides peligrosos y desplazarlos de sus órbitas años antes de que impactaran con la Tierra. Para estas misiones el motor tiene suficiente con la energía solar pero si queremos alcanzar Marte en 39 días, se necesita 1000 veces más potencia. La única manera de conseguirlo es mediante la ayuda de un reactor nuclear. Las primeras versiones de la tecnología del reactor se usaron desde la década de 1960 a 1980 por la Unión Soviética, pero no han sido usados en el espacio desde entonces y se necesitaría tiempo para su desarrollo. Resumiendo, que me da a mi en la nariz que para viajar a Marte en 39 días, harán falta 39 años.
Visto en: Newscientistthis time i contact you to see if its possible thanks to Bohms effect a high energy source and the circuit (see the pdf paper article)
to create a non habitated spacial vehicle that creates once launched into space a very high variable magnetical field order of 117 Tesla then pass near the sun in order to capture enough cosmic rays to trap and accelerate them even more to become relativistically very massive to use gravitational field so can go to Mars or in a chained way of vehicles to keep contacted to earth into deeper space , it can be useful also to deviate comets that can collide in Earth.
thank you very much and best regards.
David.
search in paper pdf for : Detection of Weak Gravitational Waves by Interferometric Methods
and Problem of Inverse Calculations
Aharonov–Bohm effect
From Wikipedia, the free encyclopedia
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–
The Aharonov–Bohm effect is important philosophically: the "classical" approach to physics is completely based on Newton's equation F = ma; so for centuries physics was all about forces, and the electric field E and the magnetic field B can be used to calculate the force on a charged particle. However, force is not a valid 4-vector in special relativity. Because of this, in special relativity it is difficult to calculate with forces. Since the E and B fields are force fields, they are also not valid special relativity 4-vectors: one can easily see this because the E and B fields one calculates or measures depend on velocity. Similarly in quantum mechanics particles are represented as waves, and it's difficult to describe how waves interact with forces. So in quantum mechanics one prefers to work with potential energy. In relativistic quantum mechanics, including quantum electro-dynamics, it's difficult to even speak of a force.
When formulating electrodynamics, one may choose to use either E and B, or the electric potential Φ and the magnetic (vector) potential A. Together, these quantities form a valid special relativistic 4-vector. However, this 4-vector is not uniquely determined, one may always add certain scalar or vector functions, derived from so-called gauge functions, to this 4-vector, and the resulting E and B fields will not change. For a long time people wondered if the A field was fundamental, even though it cannot be uniquely determined, or if it was just a mathematical trick.
The Aharonov–Bohm effect shows that you can change measurable things by passing an electron through a region that has zero E and B fields but a non-zero A field. Thus the Aharonov–Bohm effect validates the view that forces are an improper way to formulate physics, and we must use potential energy instead. In fact Richard Feynman complained that he had been taught electromagnetism from the perspective of E and B, and he wished later in life he had been taught to think in terms of the A field instead, as this would be more fundamental. The A field directly changes the phase of an electron wave function, and it is these changes in phase that lead to measurable quantities.
The Aharonov–Bohm solenoid effect, described below, demonstrates clearly that passing an electron through a region with zero E and B field, and therefore no electromagnetic forces, but non-zero A field, changes the phase of the wave function and is measurable.
The Aharonov–Bohm effect shows that the local E and B fields do not contain full information about the electromagnetic field, and the electromagnetic four-potential, A, must be used instead. By Stokes' theorem, the magnitude of the Aharonov–Bohm effect can be calculated using A alone, or using E plus B alone. But when using the fields, the effect depends on the field values in a region from which the test particle is excluded, not only classically but also quantum mechanically. In contrast, the effect depends on A only in the region where the test particle is allowed. Therefore we can either abandon the principle of locality (which most physicists are reluctant to do) or we are forced to accept the realisation that the electromagnetic 4-potential - more precisely: a certain gauge invariant quantitiy, ΦB[clarification needed], formed from it - offer a more complete description of electromagnetism than the electric and magnetic fields can. In classical electromagnetism the two descriptions were equivalent. With the addition of quantum theory, though, the electromagnetic potentials Φ and A are seen as being more fundamental. [1] The E and B
Werner Ehrenberg and Raymond E. Siday first predicted the effect in 1949,[2] and similar effects were later rediscovered by Yakir Aharonov and David Bohm in 1959.[3] (After publication of the 1959 paper, Bohm was informed of Ehrenberg and Siday's work, which was acknowledged and credited in Bohm and Aharanov's subsequent 1961 paper.[4][5])
The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid experiences a phase shift as a result of the enclosed magnetic field, despite the magnetic field being zero in the region through which the particle passes. This phase shift has been observed experimentally by its effect on interference fringes. (There are also magnetic Aharonov–Bohm effects on bound energies and scattering cross sections, but these cases have not been experimentally tested.) An electric Aharonov–Bohm phenomenon was also predicted, in which a charged particle is affected by regions with different electrical potentials but zero electric field, and this has also seen experimental confirmation. A separate "molecular" Aharonov–Bohm effect was proposed for nuclear motion in multiply-connected regions, but this has been argued to be essentially different, depending only on local quantities along the nuclear path.[6] A general review can be found in Peshkin and Tonomura (1989).[7]
This effect was chosen by the New Scientist magazine as one of the seven wonders of quantum world.[8]
Contents[hide] |
[edit]Magnetic solenoid effect
The magnetic Aharonov–Bohm effect can be seen as a result of the requirement that quantum physics be invariant with respect to the gauge choice for the electromagnetic potential, of which the magnetic vector potential A forms part.
Electromagnetic theory implies that a particle with electric charge q travelling along some path P in a region with zero magnetic field B, but non-zero A (by  ), acquires a phase shift
), acquires a phase shift  , given in SI units by
, given in SI units by
 ), acquires a phase shift
), acquires a phase shift  , given in SI units by
, given in SI units by
Therefore particles, with the same start and end points, but travelling along two different routes will acquire a phase difference Δφ determined by the magnetic flux ΦB through the area between the paths (via Stokes' theorem and 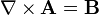 ), and given by:
), and given by:
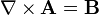 ), and given by:
), and given by:
In quantum mechanics the same particle can travel between two points by a variety of paths. Therefore this phase difference can be observed by placing a solenoid between the slits of a double-slit experiment (or equivalent). An ideal solenoid encloses a magnetic field B, but does not produce any magnetic field outside of its cylinder, and thus the charged particle (e.g. an electron) passing outside experiences no magnetic field B. However, there is a (curl-free) vector potential A outside the solenoid with an enclosed flux, and so the relative phase of particles passing through one slit or the other is altered by whether the solenoid current is turned on or off. This corresponds to an observable shift of the interference fringes on the observation plane.
The same phase effect is responsible for the quantized-flux requirement in superconducting loops. This quantization occurs because the superconducting wave function must be single valued: its phase difference Δφ around a closed loop must be an integer multiple of 2π (with the charge for the electron Cooper pairs), and thus the flux Φ must be a multiple of h/2e. The superconducting flux quantum was actually predicted prior to Aharonov and Bohm, by F. London in 1948 using a phenomenological model.[9]
The magnetic Aharonov–Bohm effect was experimentally confirmed by Osakabe et al. (1986),[10] following much earlier work summarized in Olariu and Popèscu (1984).[11] Its scope and application continues to expand. Webb et al. (1985)[12] demonstrated Aharonov–Bohm oscillations in ordinary, non-superconducting metallic rings; for a discussion, see Schwarzschild (1986)[13] and Imry & Webb (1989).[14]Bachtold et al. (1999)[15] detected the effect in carbon nanotubes; for a discussion, see Kong et al. (2004).[16]
[edit]Monopoles and Dirac strings
The magnetic Aharonov–Bohm effect is also closely related to Dirac's argument that the existence of a magnetic monopole can be accommodated by the existing magnetic source-free Maxwell's equations if both electric and magnetic charges are quantized.
A magnetic monopole implies a mathematical singularity in the vector potential, which can be expressed as an Dirac string of infinitesimal diameter that contains the equivalent of all of the 4πg flux from a monopole "charge" g. The Dirac string starts from, and terminates on, a magnetic monopole. Thus, assuming the absence of an infinite-range scattering effect by this arbitrary choice of singularity, the requirement of single-valued wave functions (as above) necessitates charge-quantization. That is,  must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
 must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
must be an integer (in cgs units) for any electric charge qe and magnetic charge qm.
Like the electromagnetic potential A the Dirac string is not gauge invariant (it moves around with fixed endpoints under a gauge transformation) is also not directly measurable.
[edit]Electric effect
Just as the phase of the wave function depends upon the magnetic vector potential, it also depends upon the scalar electric potential. By constructing a situation in which the electrostatic potential varies for two paths of a particle, through regions of zero electric field, an observable Aharonov–Bohm interference phenomenon from the phase shift has been predicted; again, the absence of an electric field means that, classically, there would be no effect.
From the Schrödinger equation, the phase of an eigenfunction with energy E goes as 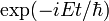 . The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
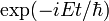 . The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
. The energy, however, will depend upon the electrostatic potential V for a particle with charge q. In particular, for a region with constant potential V(zero field), the electric potential energy qV is simply added to E, resulting in a phase shift:
where t is the time spent in the potential.
The initial theoretical proposal for this effect suggested an experiment where charges pass through conducting cylinders along two paths, which shield the particles from external electric fields in the regions where they travel, but still allow a varying potential to be applied by charging the cylinders. This proved difficult to realize, however. Instead, a different experiment was proposed involving a ring geometry interrupted by tunnel barriers, with a bias voltage V relating the potentials of the two halves of the ring. This situation results in an Aharonov–Bohm phase shift as above, and was observed experimentally in 1998.[17]
[edit]Aharonov–Bohm nano rings
Nano rings were created by accident[18] while intending to make quantum dots. They have interesting optical properties associated with excitons and the Aharonov–Bohm effect.[18] Application of these rings used as light capacitors or buffers includesphotonic computing and communications technology. Analysis and measurement of geometric phases in mesoscopic rings is ongoing.[19][20][21]
[edit]Mathematical interpretation
| This section needs additional citations for verif Please help improve this article by adding reliable references. Unsourced material may be challenged and removed. ( |
In the terms of modern differential geometry, the Aharonov–Bohm effect can be understood to be the monodromy of a flat complex line bundle. The U(1)-connection on this line bundle is given by the electromagnetic four-potential A as  where d
where d  . The curvature form of the connection,
. The curvature form of the connection, 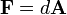 , is the electromagnetic field strength, where
, is the electromagnetic field strength, where  is the 1-form corresponding to the four-potential. The holonomy of the connection,
is the 1-form corresponding to the four-potential. The holonomy of the connection,  around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is
around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is  ; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
 where d
where d  . The curvature form of the connection,
. The curvature form of the connection, 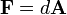 , is the electromagnetic field strength, where
, is the electromagnetic field strength, where  is the 1-form corresponding to the four-potential. The holonomy of the connection,
is the 1-form corresponding to the four-potential. The holonomy of the connection,  around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is
around a closed loop γ is, as a consequence of Stokes' theorem, determined by the magnetic flux through a surface bounded by the loop. This description is general and works inside as well as outside the conductor. Outside of the conducting tube, which is for example a longitudinally magnetized infinite metallic thread, the field strength is  ; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
; in other words outside the thread the connection is flat, and the holonomy of a loop contained in the field-free region depends only on the winding numberaround the tube and is, by definition, the monodromy of the flat connection.
In any simply connected region outside of the tube we can find a gauge transformation (acting on wave functions and connections) that gauges away the vector potential. However, if the monodromy is non trivial, there is no such gauge transformation for the whole outside region. If we want to ignore the physics inside the conductor and only describe the physics in the outside region, it becomes natural to mathematically describe the quantum electron by a section in a complex line bundle with an "external" connection  rather than an external EM field
rather than an external EM field 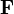 (by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
(by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
 rather than an external EM field
rather than an external EM field 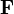 (by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
(by incorporating local gauge transformations we have already acknowledged that quantum mechanics defines the notion of a (locally) flat wavefunction (zero momentum density) but not that of unit wavefunction). The Schrödinger equation readily generalizes to this situation. In fact for the Aharonov–Bohm effect we can work in two simply connected regions with cuts that pass from the tube towards or away from the detection screen. In each of these regions we have to solve the ordinary free Schrödinger equations but in passing from one region to the other, in only one of the two connected components of the intersection (effectively in only one of the slits) we pick up a monodromy factor eiα, which results in a shift in the interference pattern.
Effects with similar mathematical interpretation can be found in other fields. For example, in classical statistical physics, quantization of a molecular motor motion in a stochastic environment can be interpreted as an Aharonov–Bohm effect induced by a gauge field acting in the space of control parameters.[22]
[edit]See also
[edit]References
- ^ Feynman, R. The Feynman Lectures on Physics. 2. p. 15-5. "knowledge of the classical electromagnetic field acting locally on a particle is not sufficient to predict its quantum-mechanical behavior. and ...is the vector potential a "real" field? ... a real field is a mathematical device for avoiding the idea of action at a distance. .... for a long time it was believed that A was not a "real" field. .... there are phenomena involving quantum mechanics which show that in fact A is a "real" field in the sense that we have defined it..... E and B are slowly disappearing from the modern expression of physical laws; they are being replaced by A[the vector potential] and
 [the scalar potential]"
[the scalar potential]" - ^ Ehrenberg, W; Siday, RE (1949). "The Refractive Index in Electron Optics and the Principles of Dynamics".Proceedings of the Physical Society B 62: 8–21.doi:10.1088/0370-1301/62/
1/303. - ^ Aharonov, Y; Bohm, D (1959). "Significance of electromagnetic potentials in quantum theory". Physical Review 115: 485–491. doi:10.1103/PhysRev.
115.485. - ^ Peat, FD (1997). Infinite Potential: The Life and Times of David Bohm. Addison-Wesley. ISBN 0-
201-40635-7. - ^ Aharonov, Y; Bohm, D (1961). "Further Considerations on Electromagnetic Potentials in the Quantum Theory".Physical Review 123: 1511–1524.doi:10.1103/PhysRev.
123.1511. - ^ Sjöqvist, E (2002). "Locality and topology in the molecular Aharonov-Bohm effect". Physical Review Letters 89 (21): 210401. doi:10.1103/
PhysRevLett.89.210401.arXiv:qu ant-ph/0112136. - ^ Peshkin, M; Tonomura, A (1989). The Aharonov-Bohm effect. Springer-Verlag. ISBN
3-540-51567-4. - ^ "Seven wonders of the quantum world", newscientist.com
- ^ London, F (1948). "On the Problem of the Molecular Theory of Superconductivity". Physical Review 74: 562.doi:10.1103/PhysRev.74.562
. - ^ Osakabe, N; et al. (1986). "Experimental confirmation of Aharonov-Bohm effect using a toroidal magnetic field confined by a superconductor". Physical Review A 34: 815.doi:10.1103/PhysRevA.34.
815. - ^ Olariu, S; Popescu, II (1985). "The quantum effects of electromagnetic fluxes". Reviews of Modern Physics 57: 339. doi:10.1103/RevModPhys.
57.339. - ^ Webb, RA; Washburn, S; Umbach, CP; Laibowitz, RB (1985). "Observation of h/e Aharonov-Bohm Oscillations in Normal-Metal Rings". Physical Review Letters 54: 2696.doi:10.1103/PhysRevLett.
54.2696. - ^ Schwarzschild, B (1986). "Currents in Normal-Metal Rings Exhibit Aharonov–Bohm Effect". Physics Today 39(1): 17. doi:10.1063/1.2814843.
- ^ Imry, Y; Webb, RA (1989). "Quantum Interference and the Aharonov-Bohm Effect". Scientific American 260 (4).
- ^ Schönenberger, C; Bachtold, Adrian; Strunk, Christoph; Salvetat, Jean-Paul; Bonard, Jean-Marc; Forró, Laszló; Nussbaumer, Thomas (1999). "Aharonov–Bohm oscillations in carbon nanotubes". Nature 397: 673.doi:10.1038/17755.
- ^ Kong, J; Kouwenhoven, L; Dekker, C (2004). "Quantum change for nanotubes". Physics World. Retrieved 2009-08-17.
- ^ van Oudenaarden, A; Devoret, Michel H.; Nazarov, Yu. V.; Mooij, J. E. (1998). "Magneto-electric Aharonov–Bohm effect in metal rings". Nature 391: 768.doi:10.1038/35808.
- ^ a b Fischer, AM (2009). "Quantum doughnuts slow and freeze light at will". Innovation Reports. Retrieved 2008-08-17.
- ^ Borunda, MF; et al. (2008). "Aharonov-Casher and spin Hall effects in two-dimensional mesoscopic ring structures with strong spin-orbit interaction". arΧiv:0809.0880
[cond-mat.mes-hall]. - ^ Grbic, B; et al. (2008). "Aharonov-Bohm oscillations in p-type GaAs quantum rings". Physica E 40: 1273.doi:10.1016/j.physe.2007.
08.129. arXiv:0711.0489. - ^ Fischer, AM; et al. (2009). "Exciton Storage in a Nanoscale Aharonov-Bohm Ring with Electric Field Tuning". Physical Review Letters 102: 096405.doi:10.1103/
PhysRevLett.102.096405. arXiv: 0809.3863. - ^ Chernyak, VY; Sinitsyn, NA (2009). "Robust quantization of a molecular motor motion in a stochastic environment".Journal of Chemical Physics 131: 181101.doi:10.1063/1.3263821.
arXiv:0906.3032.Bibcode: 2009J ChPh.131r1101C.
[edit]External links
Cosmic ray
From Wikipedia, the free encyclopedia
For the 1962 Bruce Conner film, see Cosmic Ray (film).
"cosmic radiation" redirects here, for some background types of cosmic radiation, see cosmic background radiation and cosmic background
Cosmic rays are energetic charged subatomic particles, originating from outer space, that impinge on Earth's atmosphere. They may produce secondary particles that may penetrate to the Earth's surface, and deeper. Cosmic rays are the same particles that are stable (nonradioactive) components of the types of atoms that normally occur on Earth, i.e. protons, atomic nuclei, or electrons. Cosmic rays thus resemble the particles that circulate inside particle accelerators, although cosmic ray energies may be far higher (see below). The term ray derivces from the early days of radiation research, when a directed stream of any ionizing radiation was termed a "ray" (example, alpha rays). At the time they were named, the precise nature of cosmic rays was not understood, and it was thought they might be electromagnetic radiation, like gamma rays. Cosmic ray particles are now known to arrive individually, not in the form of a beam — although a single particle can produce a directed "shower" of many secondary particles. Today, when the particle nature of cosmic rays must be emphasized, the term "cosmic ray particle" is often used.
About 89% of incoming cosmic ray particles are simple protons (hydrogen nuclei), nearly 10% are helium nuclei (alpha particles), and slightly under 1% of cosmic ray nuclei are those of the heavier elements. Solitary electrons (much like beta particles, although their ultimate source is unknown) constitute about 1% of the particles that make up galactic cosmic rays.[1]
The variety of particle energies reflects the wide variety of sources. The origins of these particles range from energetic processes on the Sun (and presumably other stars as well), to as yet unknown events in the farthest reaches of the visible universe. Cosmic rays can have energies of over 1020 eV, far higher than the 1012 to 1013 eV that man-made particle accelerators can produce. (See Ultra-high-energy cosmic rays for a description of the detection of a single particle with an energy of about 50 J, the same as a well-hit tennis ball at 42 m/s [about 150 km/h].) There has been interest in investigating cosmic rays of even greater energies.[2]
Cosmic rays have a primary role in the formation of the lithium, beryllium, and boron in the universe, through the process of "cosmic ray nucleosynthesis". They also produce some radioisotopes on Earth, such as carbon-14. In the history of science, cosmic rays were the source of the high energy reactions that resulted in the discovery of the positron, muon, and pi meson. The radiation from cosmic rays composes a large part of natural background radiation on the surface of Earth. It is far more intense outside the Earth's atmosphere and magnetic field, and because it is very difficult to shield against, is expected to have a major impact on the design of spacecraft that can safely transport humans in interplanetary space.
Contents[hide] |
[edit]Composition
Cosmic rays may broadly be divided into two categories, primary and secondary. The cosmic rays that arise in extrasolar astrophysical sources are primary cosmic rays; these primary cosmic rays can interact with interstellar matter to create secondary cosmic rays. The Sun also emits low energy cosmic rays associated with solar flares. The exact composition of primary cosmic rays, outside the Earth's atmosphere, is dependent on which part of the energy spectrum is observed. However, in general, almost 90% of all the incoming cosmic rays are protons, about 9% are helium nuclei (alpha particles) and nearly 1% are electrons. The ratio of hydrogen to helium nuclei (28% helium by mass) is about the same as the primordial elemental abundance ratio of these elements (24% by mass He) in the universe.
The remaining fraction is made up of the other heavier nuclei which are abundant end products of stars' nuclear synthesis. Secondary cosmic rays consist of the other nuclei which are not abundant nuclear synthesis end products, or products of the Big Bang, primarily lithium, beryllium, and boron. These light nuclei appear in cosmic rays in much greater abundance (about 1:100 particles) than in solar atmospheres, where their abundance is about 10−7 that of helium.
This abundance difference is a result of the way secondary cosmic rays are formed. When the heavy nuclei components of cosmic rays, namely the carbon and oxygen nuclei, collide with interstellar matter, they break up into lighter nuclei (in a process termed cosmic ray spallation) - lithium, beryllium and boron. It is found that the energy spectra of Li, Be and B fall off somewhat more steeply than those of carbon or oxygen, indicating that less cosmic ray spallation occurs for the higher energy nuclei presumably due to their escape from the galactic magnetic field. Spallation is also responsible for the abundances of scandium, titanium, vanadiu
In the past, it was believed that the cosmic ray flux has remained fairly constant over time. Recent research has, however, produced evidence for 1.5 to 2-fold millennium-timescale changes in the cosmic ray flux in the past forty thousand years.[3]
[edit]Modulation
The flux (flow rate) of cosmic rays incident on the Earth’s upper atmosphere is modulated (varied) by two processes; the Sun’s solar wind and the Earth's magnetic field. The Solar wind is expanding magnetized plasma generated by the Sun, which has the effect of decelerating the incoming particles, as well as excluding some of the particles with energies below about 1 GeV. The amount of solar wind is not constant due to changes in solar activity, for instance over its regular eleven-year cycle. Hence the level of modulation varies in anticorrelation with solar activity. Also the Earth's magnetic field deflects some of the cosmic rays, giving rise to the observation that the intensity of cosmic radiation is dependent on latitude, longitude, and azimuth angle. The cosmic flux varies from eastern and western directions due to the polarity of the Earth's geomagnetic field and the positive charge dominance in primary cosmic rays. (This is called the "east-west effect"). The cosmic-ray intensity at the Equator is lower than at the poles as the geomagnetic cutoff value is greatest at the equator. This is because charged particles tend to move in the direction of field lines and not across them, so that they are concentrated in the polar regions (where field lines are closest together). This is the reason the auroras occur at the poles, since the field lines curve down towards the Earth’s surface there. Finally, the longitude dependence arises from the fact that the geomagnetic dipole axis is not parallel to the Earth's rotation axis.
This modulation which describes the change in the interstellar intensities of cosmic rays as they propagate in the heliosphere is highly energy and spatial dependent, and it is described by the Parker's Transport Equation in the heliosphere. At large radial distances, far from the Sun (~94 AU), there exists the region where the solar wind undergoes a transition from supersonic to subsonic speeds called the "solar wind termination shock". The region between the termination shock and the heliopause (the boundary marking the end of the heliosphere) is called the heliosheath. This region acts as a barrier to cosmic rays, decreasing their intensity at lower energies by about 90%; thus it is not only the Earth's magnetic field that protects us from cosmic ray bombardment.
From a scientific modeling point of view, there is a challenge in determining the Local Interstellar Spectra (LIS) due to large adiabatic energy changes these particles experience owing to the diverging solar wind in the heliosphere. However, significant progress has been made in the field of cosmic-ray studies with the development of an improved state-of-the-art 2D numerical model that includes the simulation of the solar wind termination shock, drifts and the heliosheath coupled with fresh descriptions of the diffusion tensor, see Langner et al. (2004). Challenges also exist because the structure of the solar wind and the turbulent magnetic field in the heliosheath is not well understood indicating the heliosheath as the region unknown beyond. With lack of knowledge of the diffusion coefficient, perpendicular to the magnetic field, our knowledge of the heliosphere and from the modelling point of view is far from complete. There exist promising theories like ab initio method approaches, but the drawback is that such theories produce poor compatibility with observations (Minnie, 2006) indicating their failure in describing the mechanisms influencing the cosmic rays in the heliosphere.
[edit]Detection
The nuclei that make up cosmic rays are able to travel from their distant sources to the Earth because of the low density of matter in space. Nuclei interact strongly with other matter, so when the cosmic rays approach Earth they begin to collide with the nuclei of atmospheric gases. These collisions, in a process known as a shower, result in the production of many pions and kaons, unstable mesons which quickly decay into muons.
Because muons do not interact strongly with the atmosphere, and because of the relativistic effect of time dilation in the Earth's reference frame (alternately, length contraction in the muon's reference frame) many of these muons are able to reach the surface of the Earth and even penetrate for some distance into shallow mines. Muons are ionizing radiation, and may easily be detected by many types of particle detectors such as cloud chambers or bubble chambers or scintillation
Cosmic rays impacting other (non-Earth) bodies in the Solar System which are made of elements heavier than hydrogen and helium, can be detected indirectly by observing high energy gamma ray emissions from these bodies using a gamma-ray telescope (see image at right). When such gammas are of energy too high to result from radioactive decay processes (> about 10 MeV) they must be secondary to cosmic ray bombardment.
[edit]Detection by particle track-etch technique
Cosmic rays can also be detected directly when they pass through particle detectors flown aboard satellites or in high altitude balloons. In a pioneering technique developed by Robert Fleischer, P. Buford Price, and Robert M. Walker,[5] sheets of clear plastic such as 1/4 mil Lexan polycarbonate can be stacked together and exposed directly to cosmic rays in space or high altitude. When returned to the laboratory, the plastic sheets are "etched" [literally, slowly dissolved] in warm caustic sodium hydroxide solution, which removes the surface material at a slow, known rate. Wherever a bare cosmic ray nucleus passes through the detector, the nuclear charge causes chemical bond breaking in the plastic. The slower the particle, the more extensive is the bond-breaking along the path; and the higher the charge (the higher the Z), the more extensive is the bond-breaking along the path. The caustic sodium hydroxide dissolves at a faster rate along the path of the damage, but thereafter dissolves at the slower base-rate along the surface of the minute hole that was drilled. The net result is a conical shaped pit in the plastic; typically with two pits per sheet (one originating from each side of the plastic). The etch pits can be measured under a high power microscope (typically 1600X oil-immersion), and the etch rate plotted as a function of the depth in the stack of plastic. At the top of the stack, the ionization damage is less due to the higher speed. As the speed decreases due to deceleration in the stack, the ionization damage increases along the path. This generates a unique curve for each atomic nucleus of Z from 1 to 92, allowing identification of both the charge and energy (speed) of the particle that traverses the stack. This technique has been used with great success for detecting not only cosmic rays, but fission product nuclei for neutron detectors.
[edit]Interaction with the Earth's atmosphere
When cosmic ray particles enter the Earth's atmosphere they collide with molecules, mainly oxygen and nitrogen, to produce a cascade of lighter particles, a so-called air shower. The general idea is shown in the figure which shows a cosmic ray shower produced by a high energy proton of cosmic ray origin striking an atmospheric molecule.
This image is a simplified picture of an air shower: in reality, the number of particles created in an air shower event can reach in the billions, depending on the energy and chemical environment (i.e. atmospheric) of the primary particle. All of the produced particles stay within about one degree of the primary particle's path. Typical particles produced in such collisions are charged mesons (e.g. positive and negative pions and kaons). Cosmic rays are also responsible for the continuous production of a number of unstable isotopes in the Earth’s atmosphere, such as carbon-14, via the reaction:

Cosmic rays kept the level of carbon-14 in the atmosphere roughly constant (70 tons) for at least the past 100,000 years, until the beginning of above-ground nuclear weapons testing in the early 1950s. This is an important fact used in radiocarbon datingwhich is used in archaeology.
- Reaction products of secondary cosmic ray, lifetime and reaction[6]
- Tritium (12.3 a): 14N(n, 3H)12C (Spallation)
- Beryllium-7 (53.3 d)
- Beryllium-10 (1.6E6 a): 14N(n,p α)10Be (Spallation)
- Carbon-14 (5730 a): 14N(n, p)14C (Neutron activation)
- Sodium-22 (2.6 a)
- Sodium-24 (15 h)
- Magnesium-28 (20.9 h)
- Silicon-31 (2.6 h)
- Silicon-32 (101 a)
- Phosphorus-32 (14.3 d)
- Sulfur-35 (87.5 d)
- Sulfur-38 (2.8 h)
- Chlorine-34 m (32 min)
- Chlorine-36 (3E5 a)
- Chlorine-38 (37.2 min)
- Chlorine-39 (56 min)
- Argon-39 (269 a)
- Krypton-85 (10.7 a)
[edit]Research and experiments
See also: Cosmic-ray observatory
There are a number of cosmic ray research initiatives. These include, but are not limited to:
[edit]History
After the discovery of radioactivity by Henri Becquerel in 1896, it was generally believed that atmospheric electricity (ionization of the air) was caused only by radiation from radioactive elements in the ground or the radioactive gases (isotopes of radon) they produce. Measurements of ionization rates at increasing heights above the ground during the decade from 1900 to 1910 showed a decrease that could be explained as due to absorption of the ionizing radiation by the intervening air.
In 1909 Theodor Wulf developed an electrometer (a device to measure the rate of ion production inside a hermetically sealed container) and used it to show higher levels of radiation at the top of the Eiffel Tower than at its base, but his paper published inPhysikalische Zeitschrift was not widely accepted. In 1911 Domenico Pacini observed simultaneous variations of the rate of ionization over a lake, over the sea, and at a depth of 3 meters from the surface. Pacini concluded from the decrease of radioactivity underwater that a certain part of the ionization must be due to sources other than the radioactivity of the Earth.[7] Then, in 1912, Victor Hess carried three enhanced-accuracy Wulf electrometers[8] built in 1911 to an altitude of 5300 meters in afree balloon flight. He found the ionization rate increased approximately fourfold over the rate at ground level.[8] Hess also ruled out the Sun as the radiation's source by making a balloon ascent during a near-total eclipse. With the moon blocking much of the Sun's visible radiation, Hess still measured rising radiation at rising altitudes.[8] He concluded "The results of my observation are best explained by the assumption that a radiation of very great penetrating power enters our atmosphere from above." In 1913–1914, Werner Kolhörster confirmed Victor Hess' earlier results by measuring the increased ionization rate at an altitude of 9 km. Hess received the Nobel Prize in Physics in 1936 for his discovery.[9][10]
The term "cosmic rays" was coined by Robert Millikan who proved they were extraterrestrial in origin, and not produced by atmospheric electricity. Millikan believed that cosmic rays were high-energy photons with some secondary electrons produced byCompton scattering of gamma rays. Compton himself held the (correct) belief that cosmic rays were primarily charged particles. During the decade from 1927 to 1937, a wide variety of experimental investigations demonstrated that the primary cosmic rays are mostly positively charged particles, and the secondary radiation observed at ground level is composed primarily of a "soft component" of electrons and photons and a "hard component" of penetrating particles, muons. The muon was initially believed to be the unstable particle predicted by Hideki Yukawa in 1935 in his theory of the nuclear force. Experiments proved that the muon decays with a mean life of 2.2 microseconds into an electron and two neutrinos, but that it does not interact strongly withnuclei, so it could not be the Yukawa particle. The mystery was solved by the discovery in 1947 of the pion, which is produced directly in high-energy nuclear interactions. It decays into a muon and one neutrino with a mean life of 0.0026 microseconds. The pion→muon→electron decay sequence was observed directly in a microscopic examination of particle tracks in a special kind of photographic plate called a nuclear emulsion that had been exposed to cosmic rays at a high-altitude mountain station. In 1948, observations with nuclear emulsions carried by balloons to near the top of the atmosphere by Gottlieb and Van Allen showed that the primary cosmic particles are mostly protons with some helium nuclei (alpha particles) and a small fraction heavier nuclei.
In 1934, Bruno Rossi reported an observation of near-simultaneous discharges of two Geiger counters widely separated in a horizontal plane during a test of equipment he was using in a measurement of the so-called east-west effect. In his report on the experiment, Rossi wrote "...it seems that once in a while the recording equipment is struck by very extensive showers of particles, which causes coincidences between the counters, even placed at large distances from one another. Unfortunately, he did not have the time to study this phenomenon more closely." In 1937 Pierre Auger, unaware of Rossi's earlier report, detected the same phenomenon and investigated it in some detail. He concluded that extensive particle showers are generated by high-energy primary cosmic-ray particles that interact with air nuclei high in the atmosphere, initiating a cascade of secondary interactions that ultimately yield a shower of electrons, photons, and muons that reach ground level.
Attempts were made to measure the primary cosmic ray component at very high altitude. Soviet physicist Sergey Vernov was the first to use radiosondes to perform cosmic ray readings at high altitude. On April 1, 1935, he took measurements up to 13.6 kilometers using a pair of geiger counters in an anti-coincidence circuit to avoid counting secondary ray showers.[11][12]
Homi J. Bhabha derived an expression for the probability of scattering positrons by electrons, a process now known as Bhabha scattering. His classic paper, jointly with Walter Heitler, published in 1937 described how primary cosmic rays from space interact with the upper atmosphere to produce particles observed at the ground level. Bhabha and Heitler explained the cosmic ray shower formation by the cascade production of gamma rays and positive and negative electron pairs. In 1938 Bhabha concluded that observations of the properties of such particles would lead to the straightforward experimental verification of Albert Einstein's theory of relativity.
Measurements of the energy and arrival directions of the ultra-high-energy primary cosmic rays by the techniques of "density sampling" and "fast timing" of extensive air showers were first carried out in 1954 by members of the Rossi Cosmic Ray Group at the Massachusetts Institute of Technology. The experiment employed eleven scintillation detectors arranged within a circle 460 meters in diameter on the grounds of the Agassiz Station of the Harvard College Observatory. From that work, and from many other experiments carried out all over the world, the energy spectrum of the primary cosmic rays is now known to extend beyond 1020 eV (past the GZK cutoff, beyond which very few cosmic rays should be observed). A huge air shower experiment called the Auger Project is currently operated at a site on the pampas of Argentina by an international consortium of physicists. Their aim is to explore the properties and arrival directions of the very highest energy primary cosmic rays. The results are expected to have important implications for particle physics and cosmology. In November, 2007 preliminary results were announced showing direction of origination of the 27 highest energy events were strongly correlated with the locations of active galactic nuclei[AGN], where bare protons are believed accelerated by strong magnetic fields associated with the large black holes at the AGN centers to energies of 1020 eV and higher.
Three varieties of neutrino are produced when the unstable particles produced in cosmic ray showers decay. Since neutrinos interact only weakly with matter most of them simply pass through the Earth and exit the other side. They very occasionally interact, however, and these atmospheric neutrinos have been detected by several deep underground experiments. The Super-Kamiokande in Japan provided the first convincing evidence for neutrino oscillation in which one flavour of neutrino changes into another. The evidence was found in a difference in the ratio of electron neutrinos to muon neutrinos depending on the distance they have traveled through the air and earth.
[edit]Effects
[edit]Changes in Atmospheric Chemistry
Cosmic rays ionize the nitrogen and oxygen molecules in the atmosphere, which leads to a number of chemical reactions. One of the reactions results in ozone depletion. The magnitude of damage, however, is very small compared to the depletion caused by CFCs.
[edit]Role in ambient radiation
Cosmic rays constitute a fraction of the annual radiation exposure of human beings on the Earth. For example, the average radiation exposure in Australia is 0.3 mSv due to cosmic rays, out of a total of 2.3 mSv.[13]
[edit]Effect on electronics
Cosmic rays have sufficient energy to alter the states of elements in electronic integrated circuits, causing transient errors to occur, such as corrupted data in electronic memory devices, or incorrect performance of CPUs, often referred to as "soft errors" (not to be confused with software errors caused by programming mistakes/bugs). This has been a problem in extremely high-altitude electronics, such as in satellites, but with transistors becoming smaller and smaller, this is becoming an increasing concern in ground-level electronics as well.[14] Studies by IBM in the 1990s suggest that computers typically experience about one cosmic-ray-induced error per 256 megabytes of RAM per month.[15]
To alleviate this problem, the Intel Corporation has proposed a cosmic ray detector that could be integrated into future high-density microprocessors, allowing the processor to repeat the last command following a cosmic-ray event.[16]
Cosmic rays were recently suspected as a possible cause of a Qantas Airlines in-flight incident where an Airbus A330 airliner twice plunged hundreds of feet after an unexplained malfunction in its flight control system. Many passengers and crew members were injured, some seriously. After this incident, the accident investigators determined that the airliner's flight control system had received a data spike that could not be explained, and that all systems were in perfect working order. This has prompted a software upgrade to all A330 and A340 airliners, worldwide, so that any data spikes in this system are filtered out electronically. [17]
[edit]Significance to space travel
Main article: Health threat from cosmic rays
Galactic cosmic rays are one of the most important barriers standing in the way of plans for interplanetary travel by crewed spacecraft. Cosmic Rays also place a threat to electronics placed aboard outgoing probes. A recent malfunction aboard theVoyager 2 space probe was credited to a single flipped bit, probably caused by a cosmic ray.
[edit]Role in lightning
Cosmic rays have been implicated in the triggering of electrical breakdown in lightning. It has been proposed that essentially all lightning is triggered through a relativistic process, "runaway breakdown", seeded by cosmic ray secondaries. Subsequent development of the lightning discharge then occurs through "conventional breakdown" mechanisms.[18]
[edit]Role in climate change
A role of cosmic rays directly or via solar-induced modulations in climate change was suggested by E.P.Ney in 1959 and by Robert Dickinson in 1975. In recent years, the idea has been revived most notably by Henrik Svensmark; the most recent IPCC study disputed the mechanism,[19] while the most comprehensive review of the topic to date states: "evidence for the cosmic ray forcing is increasing as is the understanding of its physical principles."[20]
[edit]Suggested Mechanisms
Henrik Svensmark et al. have argued that solar variations modulate the cosmic ray signal seen at the Earth and that this would affect cloud formation and hence climate. Cosmic rays have been experimentally determined to be able to produce ultra-small aerosol particles,[21] orders of magnitude smaller than cloud condensation nuclei (CCN).
According to a report about an ongoing CERN CLOUD research project[22] to detect any Cosmic ray forcing is challenging since on wide spread time scales changes in the Sun’s magnetic activity, Earth’s magnetic field, and the galactic environment have to be taken into account. Empirically, increased galactic cosmic ray (GCR) flux seem to be associated with a cooler climate, a southerly shift of the ITCZ (Inter Tropical Convergence Zone)[citation needed] and a weakening of monsoon rainfalls and vice versa.[22] Claims have been made of identification of GCR climate signals in atmospheric parameters such as high latitude precipitation (Todd & Kniveton), and Svensmark's annual cloud cover variations, which were said to be correlated to GCR variation. Various proposals have been made for the mechanism by which cosmic rays might affect clouds, including ion mediated nucleation, and indirect effects on current flow density in the global electric circuit (see Tinsley 2000, and F. Yu 1999).... Other studies refer to the formation of relatively highly charged aerosols and cloud droplets at cloud boundaries, with an indirect effect on ice particle formation and altering aerosol interaction with cloud droplets.[22] Kirkby (2009) reviews developments and describes further cloud nucleation mechanisms which appear energetically favorable and depend on GCRs.[23],[24]
[edit]Geochemical and astrophysical evidence
Nir Shaviv has argued that climate signals on geological time scales are attributable to changing positions of the galactic spiral arms of the Milky Way Galaxy, and that cosmic ray flux variability is the dominant "climate driver" over these time periods.[26] Nir Shaviv and Jan Veizer in 2003[27] argue, that in contrast to a carbon based scenario, the model and proxy based estimates of atmospheric CO2 levels especially for the early Phanerozoic (see diagrams) do not show correlation with the paleoclimate picture that emerged from geological criteria, while cosmic ray flux would do.
The 2007 IPCC reports, however, strongly attribute a major role of anthropogenic carbon dioxide in the ongoing global warming, but as "different climate changes in the past had different causes" a driving role of carbon dioxide in the geological past is neither focus of the IPCC nor purported. Similarly, according a BBC report a 2008 Lancaster University study produced "further compelling evidence showing that modern-day climate change is not caused by changes in the Sun's activity".[28]
A comprehensive study of different research institutes was published 2007 by Scherer et al. in Space Science Reviews 2007.[29] The study combines geochemical evidence both on temperature, cosmic rays influence and as well astrophysical deliberations suggesting a major role in climate variability over different geological time scales. Proxy data of CRF influence comprise among others isotopic evidence in sediments on the Earth and as well changes in (iron) meteorites.
Lacking evidence of an accepted mechanism relating cosmic ray and climate e.g. via cloud cover variation and the challenges to obtain correct historical data on cosmic ray flux at various ranges of energies still lead to controversies[30]
See-also Global warming#Solar variation.
[edit]See also
- Environmental radioactivity
- Cosmic ray spallation
- Gilbert Jerome Perlow
- Ultra-high-energy cosmic ray
- Galactic cosmic ray
- Extragalactic cosmic ray
- Solar energetic particle
- Track Imaging Cherenkov Experiment
[edit]Notes
- ^ Mewaldt, R. A.. "Cosmic rays". California Institute of Technology. Retrieved 22 August 2010.
- ^ L. Anchordoqui, T. Paul, S. Reucroft, J. Swain (2003). "Ultrahigh Energy Cosmic Rays: The state of the art before the Auger Observatory". International Journal of Modern Physics A 18 (13): 2229. doi:10.1142/
S0217751X03013879. arXiv:hep- ph/0206072. - ^ D. Lal, A.J.T. Jull, D. Pollard, L. Vacher (2005). "Evidence for large century time-scale changes in solar activity in the past 32 Kyr, based on in-situ cosmogenic 14C in ice at Summit, Greenland". Earth and Planetary Science Letters 234 (3–4): 335–249. doi:10.1016/j.epsl.
2005.02.011. - ^ "EGRET Detection of Gamma Rays from the Moon". NASA/GSFC. 1 August 2005. Retrieved 2010-02-11.
- ^ R.L. Fleischer, P.B. Price, R.M. Walker (1975). Nuclear tracks in solids: Principles and applications. University of California Press.
- ^ "Natürliche, durch kosmische Strahlung laufend erzeugte Radionuklide". Retrieved 2010-02-11. (German)
- ^ D. Pacini (1912). "La radiazione penetrante alla superficie ed in seno alle acque". Il Nuovo Cimento, Series VI, 3: 93–100.doi:10.1007/BF02957440.
- ^ a b c Nobel Prize in Physics 1936 - Presentation Speech
- ^ V.F. Hess (1936). "The Nobel Prize in Physics 1936". The Nobel Foundation. Retrieved 2010-02-11.
- ^ V.F. Hess (1936). "Unsolved Problems in Physics: Tasks for the Immediate Future in Cosmic Ray Studies". Nobel Lectures. The Nobel Foundation. Retrieved 2010-02-11.
- ^ J.L. DuBois, R.P. Multhauf, C.A. Ziegler (2002). The Invention and Development of the Radiosonde. Smithsonian Studies in History and Technology. 53. Smithsonian Institution Press.
- ^ S. Vernoff (1935). "Radio-Transmission of Cosmic Ray Data from the Stratosphere". Nature 135: 1072.doi:10.1038/1351072c0.
- ^ http://www.arpansa.gov.au/
pubs/baseline/bg_rad.pdf - ^ IBM experiments in soft fails in computer electronics (1978-1994), from Terrestrial cosmic rays and soft errors, IBM Journal of Research and Development, Vol. 40, No. 1, 1996. Retrieved April 16, 2008.
- ^ Scientific American (2008-07-21). "Solar Storms: Fast Facts". Nature Publishing Group. Retrieved 2009-12-08.
- ^ Intel plans to tackle cosmic ray threat, BBC News Online, 8 April 2008. Retrieved April 16, 2008.
- ^ Cosmic rays may have hit Qantas plane of the coast of North West Australia, News.com.au, 18 November 2009. Retrieved 19 November, 2009.
- ^ Runaway Breakdown and the Mysteries of Lightning, Physics Today, May 2005.
- ^ Changes in Atmospheric Constituents and in Radiative Forcing IPCC Fourth Assessment Report Working Group I Report "The Physical Science Basis" 2007 [1]
- ^ K. Scherer, H. Fichtner et al. (December, 2006). "Interstellar-Terrestrial Relations: Variable Cosmic Environments, The Dynamic Heliosphere, and Their Imprints on Terrestrial Archives and Climate". Space Science Reviews (Springer Netherlands)127. doi:10.1007/
s11214-006-9126-6. ISSN 0038- 6308. - ^ Henrik Svensmark, Jens Olaf Pepke Pedersen, Nigel Marsh, Martin Enghoff and Ulrik Uggerhøj, "Experimental Evidence for the role of Ions in Particle Nucleation under Atmospheric Conditions", Proceedings of the Royal Society A, (Early Online Publishing), 2006.
- ^ a b c Kirkby, J. 2008. Cosmic rays and climate. Surveys in Geophysics 28: 333-375)
- ^ Cosmic Rays and Climate Video Jasper Kirkby, CERN Colloquium, 4 June 2009
- ^ Cosmic Rays and Climate Presentation Jasper Kirkby, CERN Colloquium, 4 June 2009
- ^ Similar displays in Veizer and Shaviv 2003 and in 2001 IPCC Mitchell report
- ^ [2], [3]sciencebits.com/
CO2orSolar Science bit display of Nir Shaviv papers - ^ N.J. Shaviv, J. Veizer (2003). "Celestial driver of Phanerozoic climate?". GSA Today 7 (7): 4–10.
- ^ R. Black (3 April 2008). "'No Sun link' to climate change". BBC News. Retrieved 2010-02-11.
- ^ K. Scherer et al. (2006). "Interstellar-Terrestrial Relations: Variable Cosmic Environments, The Dynamic Heliosphere, and Their Imprints on Terrestrial Archives and Climate". Space Science Reviews 127 (1-4): 327. doi:10.1007/s11214-006-
9126-6.Bibcode: 2006SSRv..127. .327S. - ^ sciencebits.com/
ClimateDebate
[edit]References
- R.G. Harrison and D.B. Stephenson, Detection of a galactic cosmic ray influence on clouds, Geophysical Research Abstracts, Vol. 8, 07661, 2006 SRef-ID: 1607-7962/gra/EGU06-A-07661
- C. D. Anderson and S. H. Neddermeyer, Cloud Chamber Observations of Cosmic Rays at 4300 Meters Elevation and Near Sea-Level, Phys. Rev 50, 263,(1936).
- M. Boezio et al., Measurement of the flux of atmospheric muons with the CAPRICE94 apparatus, Phys. Rev. D 62, 032007, (2000).
- R. Clay and B. Dawson, Cosmic Bullets, Allen & Unwin, 1997. ISBN 1-86448-204-4
- T. K. Gaisser, Cosmic Rays and Particle Physics, Cambridge University Press, 1990. ISBN 0-521-32667-2
- P. K. F. Grieder, Cosmic Rays at Earth: Researcher’s Reference Manual and Data Book, Elsevier, 2001. ISBN 0-444-50710-8
- A. M. Hillas, Cosmic Rays, Pergamon Press, Oxford, 1972 ISBN 0-08-016724-1
- J. Kremer et al., Measurement of Ground-Level Muons at Two Geomagnetic Locations, Phys. Rev. Lett. 83, 4241, (1999).
- S. H. Neddermeyer and C. D. Anderson, Note on the Nature of Cosmic-Ray Particles, Phys. Rev. 51, 844, (1937).
- M. D. Ngobeni and M. S. Potgieter, Cosmic ray anisotropies in the outer heliosphere, Advances in Space Research, 2007.
- M. D. Ngobeni, Aspects of the modulation of cosmic rays in the outer heliosphere, M.Sc Dissertation, Northwest University (Potchefstroom campus) South Africa 2006.
- D. Perkins, Particle Astrophysics, Oxford University Press, 2003. ISBN 0-19-850951-0
- C. E. Rolfs and S. R. William, Cauldrons in the Cosmos, The University of Chicago Press, 1988. ISBN 0-226-72456-5
- B. B. Rossi, Cosmic Rays, McGraw-Hill, New York, 1964.
- Martin Walt, Introduction to Geomagnetically Trapped Radiation, 1994. ISBN 0-521-43143-3
- J. F. Ziegler, The Background In Detectors Caused By Sea Level Cosmic Rays, Nuclear Instruments and Methods 191, 419, (1981).
- TRACER Long Duration Balloon Project: the largest cosmic ray detector launched on balloons.
[edit]External links
| Wikimedia Commons has media related to: Cosmic rays |
- Aspera European network portal
- Animation about cosmic rays on astroparticle.org
- Particle Data Group review of Cosmic Rays by C. Amsler et al., Physics Letters B667, 1 (2008).
- Introduction to Cosmic Ray Showers by Konrad Bernlöhr.
- NOAA FTP: Lal, D., et al., 2005. Data on cosmic ray flux derived from C14 concentrations in the GISP2 Greenland ice core.
- BBC news, Cosmic rays find uranium, 2003.
- BBC news, Rays to nab nuclear smugglers, 2005.
- BBC news, Physicists probe ancient pyramid (using cosmic rays), 2004.
- Shielding Space Travelers by Eugene Parker.
- Anomalous cosmic ray hydrogen spectra from Voyager 1 and 2
- Anomalous Cosmic Rays (From NASA's Cosmicopia)
- Review of Cosmic Rays
- Composition of Solar cosmic rays
- "Who's Afraid of a Solar Flare? Solar activity can be surprisingly good for astronauts." October 7, 2005, at Science@NASA]
- History of Cosmic Rays
- Amateur Muon Detector - schematics and articles
Good Evening Mr Professor and Associate
Casimireffect with/without magnetic field to generate elevtrical energy.
http://web.njit.edu/~sirenko/
18 feb (hace 2 días)
|
the aislant film due needs to be very thin can be a nanotube carbon several films gap enough to not touch the semiconductor bands due to small dilatation thin enoug to be very close to proportionate enough attractive force due casimir effect, if the system needs small refrigaration consider also use a material like magnetorefigeration material and aportion of the Vgenerated to create a magnetical field to cold
18 feb (hace 2 días)
|
if with the configuration i show the laminate just bends try npn-npn or pnp-pnp not npn-pnp another thing would be nice p>0 refractive index n<0 refractive index areas-> sum forces=0 try it edison have to sent to trash 1000 bulbs to get one that works!!
19 feb (1 día antes)
|
the effect casimir is given in perfect Electromagnetic vaccum, consider applying a constant magnetic field opposed to the terrestrial,earth magnetic field so EM vacuum keeps perfect so more thermodynamics performance is obtained.
thank you very much and best regards.
how rector of university of kobe signs eichi Kimura, that the beauty of your heart lightened yoiur soul.
2011/2/18 Daguel none
if with the configuration i show the laminate just bends try npn-npn or pnp-pnp not npn-pnp another thing would be nice p>0 refractive index n<0 refractive index areas-> sum forces=0 try it edison have to sent to trash 1000 bulbs to get one that works!!
the aislant film due needs to be very thin can be a nanotube carbon several films gap enough to not touch the semiconductor bands due to small dilatation thin enoug to be very close to proportionate enough attractive force due casimir effect, if the system needs small refrigaration consider also use a material like magnetorefigeration material and aportion of the Vgenerated to create a magnetical field to cold
2011/2/18 Daguel none
Good Evening Mr Professor and AssociateCasimireffect with/without magnetic field to generate elevtrical energy.http://web.njit.edu/~sirenko/PapersNJIT/Ravi_IPT_2007.pdf
19 feb (1 día antes)
|
ite variation of casimir effect can be used to detect earth waves ,movement of tectonic magma plates, so can be used in conjuction with josephson effect to detect earthquakes
the efect kasimir can work better at high temperatures
http://physicsworld.com/cws/
http://physicsworld.com/cws/
19 feb (1 día antes)
|
also can be used to obtain energy from the earth weak magnetic field with small variations of it fue josephson effect joint and perpetual oscilator casimir effect :) as an alternative to the transistors coupled
20:58 (hace 22 horas)
|
all we have seen in my mails affects directly to torus high energy fussion and to cold fussion due to Waan der vaals forces between Deuterium,normal water and tritium i bet that with ions of heavy water one for isotope H20+1 neutron to each H H2O +2 neutron each Hidrogen being abel to create a magnetic field that due to masses makes H20+1 oscillates in helix very close to H20+2 aslo oscilllating in helix into the same direction but separated produces from low nuclei ineraction , if we measure casimir effect plates wave oscilation its result is the promedia,sum wave_subi/N of the oscilations of the muclear network and its independant for stand alone pure nuclei, [but "now im dreaming" we are able to detect the promedia oscillation of a stand alone nuclei giving by casimie ffect weak interaction a cuantity of movement Hn where Hn is the harmonic freq for gap nuclei gap n as resonator freq,process of fussion turns on]
thank you very much for having paid your precious time to my "conclusions", best regards. and have a nice sunday.
thank you very much for having paid your precious time to my "conclusions", best regards. and have a nice sunday.
David
Casimir effect
From Wikipedia, the free encyclopedia
In quantum field theory, the Casimir effect and the Casimir-Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, placed a few micrometers apart, without any external electromagnetic field. In a classical description, the lack of an external field also means that there is no field between the plates, and no force would be measured between them.[1] When this field is instead studied using quantum electrodynamics, it is seen that the plates do affect the virtual photons which constitute the field, and generate a net force[2]—either an attraction or a repulsion depending on the specific arrangement of the two plates. Although the Casimir effect can be expressed in terms of virtual particles interacting with the objects, it is best described and more easily calculated in terms of the zero-point energy of a quantized field in the intervening space between the objects. This force has been measured, and is a striking example of an effect purely due to second quantization.[3][4] However, the treatment of boundary conditions in these calculations has led to some controversy. In fact "Casimir's original goal was to compute the van der Waals force between polarizable molecules" of the metallic plates. Thus it can be interpreted without any reference to the zero-point energy (vacuum energy) or virtual particles of quantum fields.[5]
Dutch physicists Hendrik B. G. Casimir and Dirk Polder proposed the existence of the force and formulated an experiment to detect it in 1948 while participating in research at Philips Research Labs. The classic form of the experiment, described above, successfully demonstrated the force to within 15% of the value predicted by the theory.[6]
Because the strength of the force falls off rapidly with distance, it is only measurable when the distance between the objects is extremely small. On a submicrometre scale, this force becomes so strong that it becomes the dominant force between uncharged conductors. In fact, at separations of 10 nm—about 100 times the typical size of an atom—the Casimir effect produces the equivalent of 1 atmosphere of pressure (101.325 kPa), the precise value depending on surface geometry and other factors.[7]
In modern theoretical physics, the Casimir effect plays an important role in the chiral bag model of the nucleon; and in applied physics, it is significant in some aspects of emerging microtechnologies andnanotechnologies.[8]
for graphene without inner structures at each hexagonal cluster but with this kind of circular pattern the cuantical sink appears at its center if connected to ground so minimum of energy goes radially from outside to the center if is ground released the film behaves like a charge membrane in which can be measured 2d waves its like a topological computer it can be used effect moesser to detect by release gamma rays at applying X rays at isotopical graphene at its resonator atomic structure the oscillation position of the membrane.
same analogy but this time in a non-circular, squared cell, by repetitions od pattern a processor is created (underlying figure at red,blue red means dopated N cells blue dopated P alterned) in this case should be detected the holes and hills of the voltage (center of strred pattern) /center of circular pattern) that depending on boundary conditions can be a sink or generator of E field voltage 0-4.5V
The analogy but this time with nanotubes and configurable and programable P N P,N P N layer it works as well as lcd displays has a squared cell that groups several nanotubes that after aplying a z-index positive or negative E field makes the near nanotubes to move upwards or downwards polarizing and behaving as a promedia for each cell as a P or N block (composed of many NP,PN outside PN,NP inner respectively displaced) then once configurated the pattern of blocks the blocks behave as same as above pictures,
note at down picture any configuration can be taken, for example superposition of patterns:
i.e. above topological squared + the same moved 1/2 down and right, as simulator of qubit or again a membrane simulator based on submembranes simulator so superimposing two circled patterns we obtain a two qubit simulator by nxn superposition nxn qubits being the countour conditions of one pattern the singular maximum minimum sink hill of the others and viceversa.








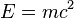



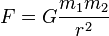
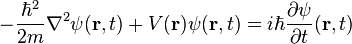

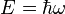


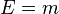

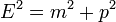



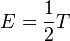

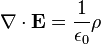
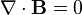
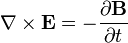
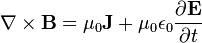
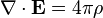















No hay comentarios:
Publicar un comentario
Ayudenos a mejorar el blog con su opinion...