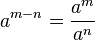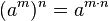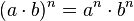solution of sequence of prime numbers:
1|basepk=((m^a*n^b*..*z^e)+1)|base10; 1=((m^a*n^b*..*z^e)+1)|base((m^a*n^b*..*z^e)+1) if
pk|basepk=1 ((m^a*n^b*..*z^e))|base((m^a*n^b*..*z^e))=
a*b base 10=a|baseb*b|basea=11|(base ab-1)
1|base((m^a*n^b*..*z^e)+1)->1|m0..(a_times+1_zeroes)..m|base(m)*n0..(b_times+1_zeroes)..n|basen*..*z0..(e_times+1_zeroes)..e|basez=
(((a_times+1_zeroes)..m|base(m)*n0..(b_times+1_zeroes)..n|basen)*z0..(e_times+1_zeroes)..e|basez/(a_times+1_zeroes)..m|base(mnz)*n0..(b_times+1_zeroes)..n|basemn..z)*..*z0..(e_times+1_zeroes)..e|basemn..z=|basepkroot(a*b*..*e)
Identities and properties
The most important identity satisfied by integer exponentiation is
This identity has the consequence
for a ≠ 0, and
Another basic identity is
((m^a*n^b*..*z^e)|base((m^a*n^b*..*z^e))+1|base((m^a*n^b*..*z^e))=11 m^a|basem=m0..(a_times_zeroes)..0->m^a=1|base(m^a)
m0..(a_times_zeroes)..0*n0..(b_times_zeroes)..0*..*z0..(e_times_zeroes)..0
m*n|base(m*n)=1->m|basen=1/(n|basem)
changing to base 2 binary and eliminating 0=/2 in base 3 /3 etc
a power base n*n=20->base10|n*n it is trivial to solve
Q where Q is a prime number
proof
(pk)-1 mod 2^a*3^b*5^c*..*(pk-1)^z=0 thats Aresthotenes cribe
((2^a*3^b*..*(pk-1)^z)|base((2^a*3^b*..*(pk-1)^z))
2^a=1|base(2^a)
10..(a_times_zeroes)..0*20..(b_times_zeroes)..0*..*(pk-1)0..(e_times_zeroes)..0
m*n|base(m*n)=1->m|basen=1/(n|basem)
(z_times+1_zeroes)..z|basepk-1/
(2_atimes+1_zeroes)..2|base(a*b*..*z)*n0..(3_btimes+1_zeroes)..3|basea*b*..*z)*..*z0..(5_times+1_zeroes)..5|basea*b*..*z=|basepk^root(a*b*..*z)
we also can have limits to a b c d ... z
2^a+1=pk is the limit superior of a
exist infinite prime based numbers of merssene
3^b+1=pk
...
and so on
thus the solution of zeroes of hipothesis of riemman results trivial also
(1+1/pk^pk*S+..+1/pk^N*pk*S)=0 2^a+1=pk=S=a/2;(2^(S*2)*2^(S*2)=2^(S*2)*2^(S*4)*2^(S*4)...)/(pk-1)=0 and so on
and last fermat theorem a^n+b^n=c^n-> n=1 (pk+pnk)-1 mod 2^a*3^b*5^c*..*(pk-1+pnk-1))^z=0=(pmk-1) mod 2^a*3^b*5^c*..*(pmk-1)^z=0
means can be decomposed into a sum as well proof conjecture of goldback
Proofs for specific exponents
Main article: Proof of Fermat's Last Theorem for specific exponents
Only one mathematical proof by Fermat has survived, in which Fermat uses the technique of infinite descent to show that the area of a right triangle with integer sides can never equal the square of an integer.[21]His proof is equivalent to demonstrating that the equation
has no primitive solutions in integers (no pairwise coprime solutions). In turn, this proves Fermat's Last Theorem for the case n=4, since the equation a4 + b4 = c4 can be written as c4 − b4 = (a2)2. Alternative proofs of the case n = 4 were developed later[22] by Frénicle de Bessy (1676),[23] Leonhard Euler (1738),[24] Kausler (1802),[25] Peter Barlow (1811),[26] Adrien-Marie Legendre (1830),[27] Schopis (1825),[28]Terquem (1846),[29] Joseph Bertrand (1851),[30] Victor Lebesgue (1853, 1859, 1862),[31] Theophile Pepin (1883),[32] Tafelmacher (1893),[33] David Hilbert (1897),[34] Bendz (1901),[35] Gambioli (1901),[36] Leopold Kronecker (1901),[37] Bang (1905),[38] Sommer (1907),[39] Bottari (1908),[40] Karel Rychlík (1910),[41] Nutzhorn (1912),[42] Robert Carmichael (1913),[43] Hancock (1931),[44] and Vrǎnceanu (1966).[45]
After Fermat proved the special case n = 4, the general proof for all n required only that the theorem be established for all odd prime exponents.[46] In other words, it was necessary to prove only that the equationap + bp = cp has no integer solutions (a, b, c) when p is an odd prime number. This follows because a solution (a, b, c) for a given n is equivalent to a solution for all the factors of n. For illustration, let n be factored into d and e, n = de. The general equation
- an + bn = cn
implies that (ad, bd, cd) is a solution for the exponent e
- (ad)e + (bd)e = (cd)e
Thus, to prove that Fermat's equation has no solutions for n > 2, it suffices to prove that it has no solutions for at least one prime factor of every n. All integers n > 2 contain a factor of 4, or an odd prime number, or both. Therefore, Fermat's Last Theorem can be proven for all n if it can be proven for n = 4 and for all odd primes p.
In the two centuries following its conjecture (1637–1839), Fermat's Last Theorem was proven for three odd prime exponents p = 3, 5 and 7. The case p = 3 was first stated by Abu Mahmud Khujandi (10th century), but his attempted proof of the theorem was incorrect.[47] In 1770, Leonhard Euler gave a proof of p = 3,[48] but his proof by infinite descent[49] contained a major gap.[50] However, since Euler himself had proven the lemma necessary to complete the proof in other work, he is generally credited with the first proof.[51] Independent proofs were published[52] by Kausler (1802)[25], Legendre (1823, 1830),[27][53] Calzolari (1855),[54] Gabriel Lamé (1865),[55] Peter Guthrie Tait (1872),[56] Günther (1878),[57] Gambioli (1901),[36] Krey (1909),[58] Rychlík (1910),[41] Stockhaus (1910),[59] Carmichael (1915),[60] Johannes van der Corput (1915),[61], Axel Thue (1917),[62] and Duarte (1944).[63] The case p = 5 was proven[64] independently by Legendre and Peter Dirichlet around 1825.[65] Alternative proofs were developed[66] by Carl Friedrich Gauss (1875, posthumous),[67] Lebesgue (1843),[68] Lamé (1847),[69] Gambioli (1901),[36][70] Werebrusow (1905),[71] Rychlík (1910),[72] van der Corput (1915),[61] and Guy Terjanian (1987).[73] The case n = 7 was proven[74]by Lamé in 1839.[75] His rather complicated proof was simplified in 1840 by Lebesgue,[76] and still simpler proofs[77] were published by Angelo Genocchi in 1864, 1874 and 1876.[78] Alternative proofs were developed by Théophile Pépin (1876)[79] and Edmond Maillet (1897).[80]
Fermat's Last Theorem has also been proven for the exponents n = 6, 10, and 14. Proofs for n = 6 have been published by Kausler,[25] Thue,[81] Tafelmacher,[82] Lind,[83] Kapferer,[84] Swift,[85] and Breusch.[86] Similarly, Dirichlet[87] and Terjanian[88] each proved the case n = 14, while Kapferer[84] and Breusch[86] each proved the case n = 10. Strictly speaking, these proofs are unnecessary, since these cases follow from the proofs for n = 3, 5, and 7, respectively. Nevertheless, the reasoning of these even-exponent proofs differs from their odd-exponent counterparts. Dirichlet's proof for n = 14 was published in 1832, before Lamé's 1839 proof for n = 7.[89]
Many proofs for specific exponents use Fermat's technique of infinite descent, which Fermat used to prove the case n = 4, but many do not. However, the details and auxiliary arguments are often ad hoc and tied to the individual exponent under consideration.[90] Since they became ever more complicated as p increased, it seemed unlikely that the general case of Fermat's Last Theorem could be proven by building upon the proofs for individual exponents.[90] Although some general results on Fermat's Last Theorem were published in the early 19th century by Niels Henrik Abel and Peter Barlow,[91][92] the first significant work on the general theorem was done by Sophie Germain.[93]
[edit]
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:
Such a number is called a Goldbach number. Expressing a given even number as a sum of two primes is called a Goldbach partition of the number. For example,
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 7 + 3 or 5 + 5
- 12 = 5 + 7
- 14 = 3 + 11 or 7 + 7
Contents
[hide]
[edit]Origins
On 7 June 1742, the German mathematician Christian Goldbach of originally Brandenburg-Prussia wrote a letter to Leonhard Euler (letter XLIII)[3] in which he proposed the following conjecture:
- Every integer which can be written as the sum of two primes, can also be written as the sum of as many primes as one wishes, until all terms are units.
He then proposed a second conjecture in the margin of his letter:
- Every integer greater than 2 can be written as the sum of three primes.
He considered 1 to be a prime number, a convention subsequently abandoned.[4] The two conjectures are now known to be equivalent, but this did not seem to be an issue at the time. A modern version of Goldbach's marginal conjecture is:
- Every integer greater than 5 can be written as the sum of three primes.
Euler replied in a letter dated 30 June 1742, and reminded Goldbach of an earlier conversation they had ("...so Ew vormals mit mir communicirt haben.."), in which Goldbach remarked his original (and not marginal) conjecture followed from the following statement
- Every even integer greater than 2 can be written as the sum of two primes,
which is thus also a conjecture of Goldbach. In the letter dated 30 June 1742, Euler stated:
Goldbach's third version (equivalent to the two other versions) is the form in which the conjecture is usually expressed today. It is also known as the "strong", "even", or "binary" Goldbach conjecture, to distinguish it from a weaker corollary. The strong Goldbach conjecture implies the conjecture that all odd numbers greater than 7 are the sum of three odd primes, which is known today variously as the "weak" Goldbach conjecture, the "odd" Goldbach conjecture, or the "ternary" Goldbach conjecture. Both questions have remained unsolved ever since, although the weak form of the conjecture appears to be much closer to resolution than the strong one. If the strong Goldbach conjecture is true, the weak Goldbach conjecture will be true by implication.[6]
[edit]Verified results
For small values of n, the strong Goldbach conjecture (and hence the weak Goldbach conjecture) can be verified directly. For instance, N. Pipping in 1938 laboriously verified the conjecture up to n ≤ 105.[7] With the advent of computers, many more small values of n have been checked; T. Oliveira e Silva is running a distributed computer search that has verified the conjecture for n ≤ 1.609*1018 and some higher small ranges up to 4*1018 (double checked up to 1*1017).[8]
[edit]Heuristic justification
Statistical considerations which focus on the probabilistic distribution of prime numbers present informal evidence in favour of the conjecture (in both the weak and strong forms) for sufficiently large integers: the greater the integer, the more ways there are available for that number to be represented as the sum of two or three other numbers, and the more "likely" it becomes that at least one of these representations consists entirely of primes.
A very crude version of the heuristic probabilistic argument (for the strong form of the Goldbach conjecture) is as follows. The prime number theorem asserts that an integer m selected at random has roughly a  chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n-m simultaneously being prime to be
chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n-m simultaneously being prime to be ![1 \big / \big [\ln m \,\ln (n-m)\big ]](http://upload.wikimedia.org/math/9/6/c/96cbc99ee6810c16db7a6b13246a56bb.png) . This heuristic is non-rigorous for a number of reasons; for instance, it assumes that the events that m and n − m are prime are statistically independent of each other. Nevertheless, if one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly
. This heuristic is non-rigorous for a number of reasons; for instance, it assumes that the events that m and n − m are prime are statistically independent of each other. Nevertheless, if one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly

Since this quantity goes to infinity as n increases, we expect that every large even integer has not just one representation as the sum of two primes, but in fact has very many such representations.
The above heuristic argument is actually somewhat inaccurate, because it ignores some dependence between the events of m and n − m being prime. For instance, if m is odd then n − m is also odd, and if m is even, then n − m is even, a non-trivial relation because (besides 2) only odd numbers can be prime. Similarly, if n is divisible by 3, and m was already a prime distinct from 3, then n − mwould also be coprime to 3 and thus be slightly more likely to be prime than a general number. Pursuing this type of analysis more carefully, Hardy and Littlewood in 1923 conjectured (as part of their famous Hardy-Littlewood prime tuple conjecture) that for any fixed c ≥ 2, the number of representations of a large integer n as the sum of c primes  with
with 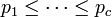 should be asymptotically equal to
should be asymptotically equal to
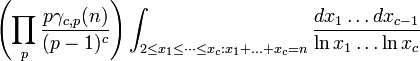
where the product is over all primes p, and γc,p(n) is the number of solutions to the equation 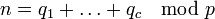 in modular arithmetic, subject to the constraints
in modular arithmetic, subject to the constraints  . This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Vinogradov, but is still only a conjecture when c = 2. In the latter case, the above formula simplifies to 0 when n is odd, and to
. This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Vinogradov, but is still only a conjecture when c = 2. In the latter case, the above formula simplifies to 0 when n is odd, and to

when n is even, where Π2 is the twin prime constant

This asymptotic is sometimes known as the extended Goldbach conjecture. The strong Goldbach conjecture is in fact very similar to the twin prime conjecture, and the two conjectures are believed to be of roughly comparable difficulty.
The Goldbach partition functions shown here can be displayed as histograms which informatively illustrate the above equations. See Goldbach's comet.[9]
[edit]Rigorous results
Considerable work has been done on the weak Goldbach conjecture.
The strong Goldbach conjecture is much more difficult. Using the method of Vinogradov, Chudakov,[10] van der Corput,[11] and Estermann[12] showed that almost all even numbers can be written as the sum of two primes (in the sense that the fraction of even numbers which can be so written tends towards 1). In 1930, Lev Schnirelmann proved that every even number n ≥ 4 can be written as the sum of at most 20 primes. This result was subsequently improved by many authors; currently, the best known result is due to Olivier Ramaré, who in 1995 showed that every even number n ≥ 4 is in fact the sum of at most six primes. In fact, resolving the weak Goldbach conjecture will also directly imply that every even number n ≥ 4 is the sum of at most four primes.[13]
Chen Jingrun showed in 1973 using the methods of sieve theory that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes)[14]—e.g., 100 = 23 + 7·11.
In 1975, Hugh Montgomery and Robert Charles Vaughan showed that "most" even numbers were expressible as the sum of two primes. More precisely, they showed that there existed positive constants c and C such that for all sufficiently large numbersN, every even number less than N is the sum of two primes, with at most CN1 − c exceptions. In particular, the set of even integers which are not the sum of two primes has density zero.
Linnik proved in 1951 the existence of a constant K such that every sufficiently large even number is the sum of two primes and at most K powers of 2. Roger Heath-Brown and Jan-Christoph Schlage-Puchta in 2002 found that K=13 works.[15] This was improved to K=8 by Pintz and Ruzsa.[16]
One can pose similar questions when primes are replaced by other special sets of numbers, such as the squares. For instance, it was proven by Lagrange that every positive integer is the sum of four squares. See Waring's problem and the relatedWaring–Goldbach problem on sums of powers of primes.
[edit]Attempted proofs
As with many famous conjectures in mathematics, there are a number of purported proofs of the Goldbach conjecture, none accepted by the mathematical community.
[edit]Similar conjectures
- Lemoine's conjecture (also called Levy's conjecture) - states that all odd integers greater than 5 can be represented as the sum of an odd prime number and an even semiprime.
- Waring–Goldbach problem - asks whether large numbers can be expressed as a sum, with at most a constant number of terms, of like powers of primes.
[edit]In popular culture
- To generate publicity for the novel Uncle Petros and Goldbach's Conjecture by Apostolos Doxiadis, British publisher Tony Faber offered a $1,000,000 prize if a proof was submitted before April 2002. The prize was not claimed.
- The television drama Lewis featured a mathematics professor who had won the Fields medal for his work on Goldbach's conjecture.
- Isaac Asimov's short story "Sixty Million Trillion Combinations" featured a mathematician who suspected that his work on Goldbach's conjecture had been stolen.
- In the Spanish movie La habitación de Fermat (2007), a young mathematician claims to have proved the conjecture.
- A reference is made to the conjecture in the Futurama straight-to-DVD film The Beast with a Billion Backs, in which multiple elementary proofs are found in a Heaven-like scenario.
- Frederik Pohl's novella "The Gold at the Starbow's End" (1972) featured a crew on an interstellar flight that solved Goldbach's conjecture.
- Michelle Richmond's novel "No One You Know" (2008) features the murder of a mathematician who had been working on solving Goldbach's conjecture.
a_ntimes0|base a+b_ntimes0|baseb=c_ntimes0|basec
a|base a*n+b|baseb*n=c|basec*n
a_atimes0|basen+b_btimes0|basen=c_timesc0|basen
solution of last fermat theorem
(a*n^a+b*n^b=c*n^c)base10
THE BEAL CONJECTURE AND PRIZE
BEAL'S CONJECTURE: If Ax +By = Cz , where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
THE BEAL PRIZE. The conjecture and prize was announced in the December 1997 issue of the Notices of the American Mathematical Society. Since that time Andy Beal has increased the amount of the prize for his conjecture. The prize is now this: $100,000 for either a proof or a counterexample of his conjecture. The prize money is being held by the American Mathematical Society until it is awarded. In the meantime the interest is being used to fund some AMS activities and the annual Erdos Memorial Lecture.
CONDITIONS FOR WINNING THE PRIZE. The prize will be awarded by the prize committee appointed by the American Mathematical Society. The present committee members are Charles Fefferman, Ron Graham, and Dan Mauldin. The requirements for the award are that in the judgment of the committee, the solution has been recognized by the mathematics community. This includes that either a proof has been given and the result has appeared in a reputable refereed journal or a counterexample has been given and verified.
PRELIMINARY RESULTS. If you have believe you have solved the problem, please submit the solution to a reputable refereed journal. If you have questions, they can be mailed to:
The Beal Conjecture and Prize
c/o Professor R. Daniel Mauldin
Department of Mathematics
Box 311430
University of North Texas
Denton, Texas 76203
Questions and queries can also be FAXED to 940-565-4805 or sent by e-mail to
a_ntimes0|base a+b_mtimes0|baseb=c_ptimes0|basec
=a|base a*n+b|baseb*m=c|basec*p
a_atimes0|basen+b_btimes0|basem=c_timesc0|basep
a*n^a|basea+b*m^b|baseb-c*p^c|basec=
n^(a+1)|basea+m^(b+1)|baseb=p^(c+1)|basec
n^(a+1)|basef*g+m^(b+1)|basef*h=p^(c+1)basef*k=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef=0
a,b,c..>impair,odd->((n^(a+1))^g),(m^(b+1))^h),(p^(c+1))^k) even
(((n^(a+1))^g+(m^(b+1))^h)-f*(p^(c+1))^k)=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef
[((((n^(a+1))^g+(m^(b+1))^h))]*f=(((n^(a+1))^g+(m^(b+1))^h)
f*g=a f*h=b f*k=c
by substituing:
[((((n^(f*g+1))^g+(m^(f*h+1))^h))]*f=(((n^(f*g+1))^g+(m^(f*h+1))^h)
f*n=n f*m=m g=a h=b k=c if (n^(1*g+1))^g=(m^(1*h+1))^h)) (g+1)^g)=(m+1)^h=(c+1))^k=i simplifies into last fermat theorem n^i+m^i=p^i
Power sum symmetric polynomial
From Wikipedia, the free encyclopedia
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Contents
[hide]
[edit]Definition
The power sum symmetric polynomial of degree k in n variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers of the variables. Formally,

The first few of these polynomials are


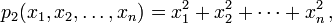

Thus, for each nonnegative integer k, there exists exactly one power sum symmetric polynomial of degree k in n variables.
The polynomial ring formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring.
[edit]Examples
The following lists the n power sum symmetric polynomials of positive degrees up to n for the first three positive values of n. In every case, p0 = n is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1:

For n = 2:
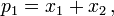

For n = 3:


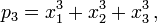
[edit]Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ring of symmetric polynomials in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) The same is true if the coefficients are taken in any field whose characteristic is 0.
The same is true if the coefficients are taken in any field whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
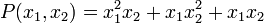
has the expression

which involves fractions. According to the theorem this is the only way to represent P(x1,x2) in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring ![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
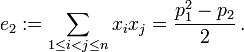
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then  , so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):

Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):

This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n. Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function  of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
[edit]References
- Macdonald, I.G. (1979), Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Oxford: Clarendon Press.
- Macdonald, I.G. (1995), Symmetric Functions and Hall Polynomials, second ed. Oxford: Clarendon Press. ISBN 0-19-850450-0 (paperback, 1998).
- Richard P. Stanley (1999), Enumerative Combinatorics, Vol. 2. Cambridge: Cambridge University Press. ISBN 0-521-56069-1
[edit]See also
Newton's identities
From Wikipedia, the free encyclopedia
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monicpolynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, includinggeneral relativity.
[edit]Mathematical statement
[edit]Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:

and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial that is the sum of all distinct products of k distinct variables, so in particular

Then the Newton's identities can be stated as

valid for all k ≥ 1. Concretely, one gets for the first few values of k:

The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has

and so on; here the left-hand sides never become zero. These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as

[edit]Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:
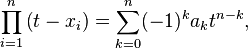
where the coefficients ak are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn). Now consider the power sums of the roots

Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
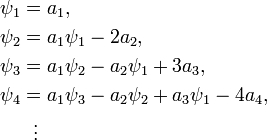
[edit]Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomial of a matrix A, the roots xi are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue xi of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is thek-th power sum ψk of the roots of the characteristic polynomial of A, is given by its trace:
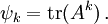
The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
[edit]Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomial expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial  with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
[edit]Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
[edit]A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomial that is the sum of all monomials of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functions, they read

valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has

These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity

The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
[edit]Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
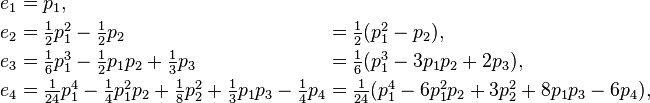
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
[edit]Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations

and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle index polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomialp1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as 1 / N where 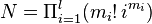 ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
[edit]Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators:
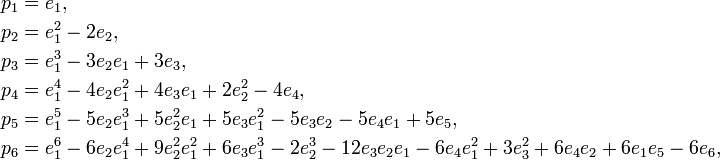
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial 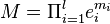 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
[edit]Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them:
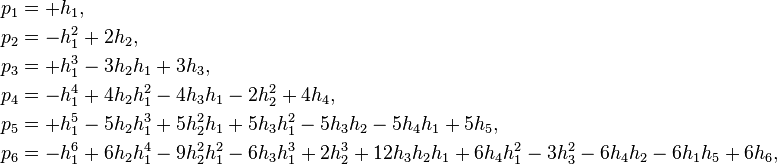
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial  is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
[edit]Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's rule to find the solution for the final unknown. For instance taking Newton's identities in the form
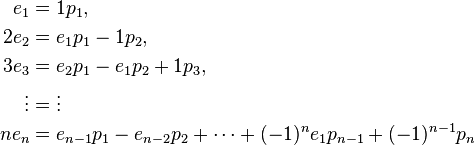
we consider p1, − p2, p3, ..., ( − 1)npn − 1 and pn as unknowns, and solve for the final one, giving

Solving for en instead of for pn is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
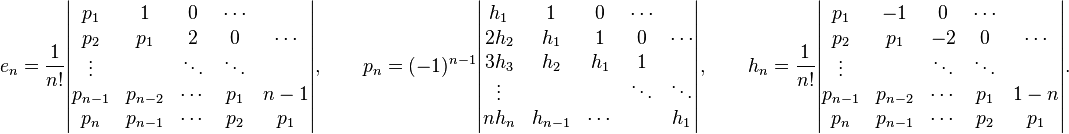
Note that the use of determinants makes that formula for hn has additional minus signs with respect to the one for en, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for hn by taking the permanent of the matrix for en instead of the determinant, and more generally an expression for any Schur polynomial can be obtained by taking the corresponding immanant of this matrix.
[edit]Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
[edit]From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into

as follows. Substituting xj for t gives

Summing over all j gives
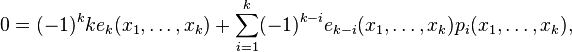
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
[edit]Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation

linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving

Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity

One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain

where the polynomial on the right hand side was first rewritten as a rational function in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains

which gives the k-th Newton identity.
[edit]As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomials of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has
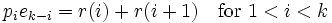
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially
 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus
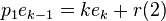 .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
[edit]See also
- Power sum symmetric polynomial
- Elementary symmetric polynomial
- Symmetric function
- Fluid solutions, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensor in the case of a perfect fluid, and similar articles on other types of exact solutions in general relativity.
[edit]References
- Tignol, Jean-Pierre (2001). Galois' theory of algebraic equations. Singapore: World Scientific. ISBN 978-981-02-4541-2.
- Bergeron, F.; Labelle, G.; and Leroux, P. (1998). Combinatorial species and tree-like structures. Cambridge: Cambridge University Press. ISBN 978-0-521-57323-8.
- Cameron, Peter J. (1999). Permutation Groups. Cambridge: Cambridge University Press. ISBN 978-0-521-65378-7.
- Cox, David; Little, John, and O'Shea, Donal (1992). Ideals, Varieties, and Algorithms. New York: Springer-Verlag. ISBN 978-0-387-97847-5.
- Eppstein, D.; Goodrich, M. T. (2007). "Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters". Algorithms and Data Structures, 10th International Workshop, WADS 2007. Springer-Verlag, Lecture Notes in Computer Science 4619. pp. 637–648. arXiv:0704.3313
- Littlewood, D. E. (1950). The theory of group characters and matrix representations of groups. Oxford: Oxford University Press. viii+310. ISBN 0-8218-4067-3.
- Macdonald, I. G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford: The Clarendon Press, Oxford University Press. viii+180. ISBN 0-19-853530-9. MR84g:05003
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (Second ed.). New York: Oxford Science Publications. The Clarendon Press, Oxford University Press. p. x+475. ISBN 0-19-853489-2.MR96h:05207
- Mead, D.G. (1992-10). "Newton's Identities". The American Mathematical Monthly (Mathematical Association of America) 99 (8): 749–751. doi:10.2307/2324242.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Vol. 2. Cambridge University Press. ISBN 0-521-56069-1 (hardback), ISBN 0-521-78987-7 (paperback).
- Sturmfels, Bernd (1992). Algorithms in Invariant Theory. New York: Springer-Verlag. ISBN 978-0-387-82445-1.
- Tucker, Alan (1980). Applied Combinatorics (5/e ed.). New York: Wiley. ISBN 978-0-471-73507-6.
[edit]External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:
Such a number is called a Goldbach number. Expressing a given even number as a sum of two primes is called a Goldbach partition of the number. For example,
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 7 + 3 or 5 + 5
- 12 = 5 + 7
- 14 = 3 + 11 or 7 + 7
Contents[hide] |
[edit]Origins
On 7 June 1742, the German mathematician Christian Goldbach of originally Brandenburg-Prussia wrote a letter to Leonhard Euler (letter XLIII)[3] in which he proposed the following conjecture:
- Every integer which can be written as the sum of two primes, can also be written as the sum of as many primes as one wishes, until all terms are units.
He then proposed a second conjecture in the margin of his letter:
- Every integer greater than 2 can be written as the sum of three primes.
He considered 1 to be a prime number, a convention subsequently abandoned.[4] The two conjectures are now known to be equivalent, but this did not seem to be an issue at the time. A modern version of Goldbach's marginal conjecture is:
- Every integer greater than 5 can be written as the sum of three primes.
Euler replied in a letter dated 30 June 1742, and reminded Goldbach of an earlier conversation they had ("...so Ew vormals mit mir communicirt haben.."), in which Goldbach remarked his original (and not marginal) conjecture followed from the following statement
- Every even integer greater than 2 can be written as the sum of two primes,
which is thus also a conjecture of Goldbach. In the letter dated 30 June 1742, Euler stated:
Goldbach's third version (equivalent to the two other versions) is the form in which the conjecture is usually expressed today. It is also known as the "strong", "even", or "binary" Goldbach conjecture, to distinguish it from a weaker corollary. The strong Goldbach conjecture implies the conjecture that all odd numbers greater than 7 are the sum of three odd primes, which is known today variously as the "weak" Goldbach conjecture, the "odd" Goldbach conjecture, or the "ternary" Goldbach conjecture. Both questions have remained unsolved ever since, although the weak form of the conjecture appears to be much closer to resolution than the strong one. If the strong Goldbach conjecture is true, the weak Goldbach conjecture will be true by implication.[6]
[edit]Verified results
For small values of n, the strong Goldbach conjecture (and hence the weak Goldbach conjecture) can be verified directly. For instance, N. Pipping in 1938 laboriously verified the conjecture up to n ≤ 105.[7] With the advent of computers, many more small values of n have been checked; T. Oliveira e Silva is running a distributed computer search that has verified the conjecture for n ≤ 1.609*1018 and some higher small ranges up to 4*1018 (double checked up to 1*1017).[8]
[edit]Heuristic justification
Statistical considerations which focus on the probabilistic distribution of prime numbers present informal evidence in favour of the conjecture (in both the weak and strong forms) for sufficiently large integers: the greater the integer, the more ways there are available for that number to be represented as the sum of two or three other numbers, and the more "likely" it becomes that at least one of these representations consists entirely of primes.
A very crude version of the heuristic probabilistic argument (for the strong form of the Goldbach conjecture) is as follows. The prime number theorem asserts that an integer m selected at random has roughly a  chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n-m simultaneously being prime to be
chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n-m simultaneously being prime to be ![1 \big / \big [\ln m \,\ln (n-m)\big ]](http://upload.wikimedia.org/math/9/6/c/96cbc99ee6810c16db7a6b13246a56bb.png) . This heuristic is non-rigorous for a number of reasons; for instance, it assumes that the events that m and n − m are prime are statistically independent of each other. Nevertheless, if one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly
. This heuristic is non-rigorous for a number of reasons; for instance, it assumes that the events that m and n − m are prime are statistically independent of each other. Nevertheless, if one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly
 chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n-m simultaneously being prime to be
chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n-m simultaneously being prime to be ![1 \big / \big [\ln m \,\ln (n-m)\big ]](http://upload.wikimedia.org/math/9/6/c/96cbc99ee6810c16db7a6b13246a56bb.png) . This heuristic is non-rigorous for a number of reasons; for instance, it assumes that the events that m and n − m are prime are statistically independent of each other. Nevertheless, if one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly
. This heuristic is non-rigorous for a number of reasons; for instance, it assumes that the events that m and n − m are prime are statistically independent of each other. Nevertheless, if one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly
Since this quantity goes to infinity as n increases, we expect that every large even integer has not just one representation as the sum of two primes, but in fact has very many such representations.
The above heuristic argument is actually somewhat inaccurate, because it ignores some dependence between the events of m and n − m being prime. For instance, if m is odd then n − m is also odd, and if m is even, then n − m is even, a non-trivial relation because (besides 2) only odd numbers can be prime. Similarly, if n is divisible by 3, and m was already a prime distinct from 3, then n − mwould also be coprime to 3 and thus be slightly more likely to be prime than a general number. Pursuing this type of analysis more carefully, Hardy and Littlewood in 1923 conjectured (as part of their famous Hardy-Littlewood prime tuple conjecture) that for any fixed c ≥ 2, the number of representations of a large integer n as the sum of c primes  with
with 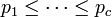 should be asymptotically equal to
should be asymptotically equal to
 with
with 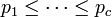 should be asymptotically equal to
should be asymptotically equal to
where the product is over all primes p, and γc,p(n) is the number of solutions to the equation 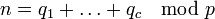 in modular arithmetic, subject to the constraints
in modular arithmetic, subject to the constraints  . This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Vinogradov, but is still only a conjecture when c = 2. In the latter case, the above formula simplifies to 0 when n is odd, and to
. This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Vinogradov, but is still only a conjecture when c = 2. In the latter case, the above formula simplifies to 0 when n is odd, and to
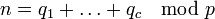 in modular arithmetic, subject to the constraints
in modular arithmetic, subject to the constraints  . This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Vinogradov, but is still only a conjecture when c = 2. In the latter case, the above formula simplifies to 0 when n is odd, and to
. This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Vinogradov, but is still only a conjecture when c = 2. In the latter case, the above formula simplifies to 0 when n is odd, and to
when n is even, where Π2 is the twin prime constant
This asymptotic is sometimes known as the extended Goldbach conjecture. The strong Goldbach conjecture is in fact very similar to the twin prime conjecture, and the two conjectures are believed to be of roughly comparable difficulty.
The Goldbach partition functions shown here can be displayed as histograms which informatively illustrate the above equations. See Goldbach's comet.[9]
[edit]Rigorous results
Considerable work has been done on the weak Goldbach conjecture.
The strong Goldbach conjecture is much more difficult. Using the method of Vinogradov, Chudakov,[10] van der Corput,[11] and Estermann[12] showed that almost all even numbers can be written as the sum of two primes (in the sense that the fraction of even numbers which can be so written tends towards 1). In 1930, Lev Schnirelmann proved that every even number n ≥ 4 can be written as the sum of at most 20 primes. This result was subsequently improved by many authors; currently, the best known result is due to Olivier Ramaré, who in 1995 showed that every even number n ≥ 4 is in fact the sum of at most six primes. In fact, resolving the weak Goldbach conjecture will also directly imply that every even number n ≥ 4 is the sum of at most four primes.[13]
Chen Jingrun showed in 1973 using the methods of sieve theory that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes)[14]—e.g., 100 = 23 + 7·11.
In 1975, Hugh Montgomery and Robert Charles Vaughan showed that "most" even numbers were expressible as the sum of two primes. More precisely, they showed that there existed positive constants c and C such that for all sufficiently large numbersN, every even number less than N is the sum of two primes, with at most CN1 − c exceptions. In particular, the set of even integers which are not the sum of two primes has density zero.
Linnik proved in 1951 the existence of a constant K such that every sufficiently large even number is the sum of two primes and at most K powers of 2. Roger Heath-Brown and Jan-Christoph Schlage-Puchta in 2002 found that K=13 works.[15] This was improved to K=8 by Pintz and Ruzsa.[16]
One can pose similar questions when primes are replaced by other special sets of numbers, such as the squares. For instance, it was proven by Lagrange that every positive integer is the sum of four squares. See Waring's problem and the relatedWaring–Goldbach problem on sums of powers of primes.
[edit]Attempted proofs
As with many famous conjectures in mathematics, there are a number of purported proofs of the Goldbach conjecture, none accepted by the mathematical community.
[edit]Similar conjectures
- Lemoine's conjecture (also called Levy's conjecture) - states that all odd integers greater than 5 can be represented as the sum of an odd prime number and an even semiprime.
- Waring–Goldbach problem - asks whether large numbers can be expressed as a sum, with at most a constant number of terms, of like powers of primes.
[edit]In popular culture
- To generate publicity for the novel Uncle Petros and Goldbach's Conjecture by Apostolos Doxiadis, British publisher Tony Faber offered a $1,000,000 prize if a proof was submitted before April 2002. The prize was not claimed.
- The television drama Lewis featured a mathematics professor who had won the Fields medal for his work on Goldbach's conjecture.
- Isaac Asimov's short story "Sixty Million Trillion Combinations" featured a mathematician who suspected that his work on Goldbach's conjecture had been stolen.
- In the Spanish movie La habitación de Fermat (2007), a young mathematician claims to have proved the conjecture.
- A reference is made to the conjecture in the Futurama straight-to-DVD film The Beast with a Billion Backs, in which multiple elementary proofs are found in a Heaven-like scenario.
- Frederik Pohl's novella "The Gold at the Starbow's End" (1972) featured a crew on an interstellar flight that solved Goldbach's conjecture.
- Michelle Richmond's novel "No One You Know" (2008) features the murder of a mathematician who had been working on solving Goldbach's conjecture.
solution of last fermat theorem
(a*n^a+b*n^b=c*n^c)base10
THE BEAL CONJECTURE AND PRIZE
BEAL'S CONJECTURE: If Ax +By = Cz , where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
THE BEAL PRIZE. The conjecture and prize was announced in the December 1997 issue of the Notices of the American Mathematical Society. Since that time Andy Beal has increased the amount of the prize for his conjecture. The prize is now this: $100,000 for either a proof or a counterexample of his conjecture. The prize money is being held by the American Mathematical Society until it is awarded. In the meantime the interest is being used to fund some AMS activities and the annual Erdos Memorial Lecture.
CONDITIONS FOR WINNING THE PRIZE. The prize will be awarded by the prize committee appointed by the American Mathematical Society. The present committee members are Charles Fefferman, Ron Graham, and Dan Mauldin. The requirements for the award are that in the judgment of the committee, the solution has been recognized by the mathematics community. This includes that either a proof has been given and the result has appeared in a reputable refereed journal or a counterexample has been given and verified.
PRELIMINARY RESULTS. If you have believe you have solved the problem, please submit the solution to a reputable refereed journal. If you have questions, they can be mailed to:
The Beal Conjecture and Prize
c/o Professor R. Daniel Mauldin
Department of Mathematics
Box 311430
University of North Texas
Denton, Texas 76203
Questions and queries can also be FAXED to 940-565-4805 or sent by e-mail to
a_ntimes0|base a+b_mtimes0|baseb=c_ptimes0|basec
=a|base a*n+b|baseb*m=c|basec*p
a_atimes0|basen+b_btimes0|basem=c_timesc0|basep
a*n^a|basea+b*m^b|baseb-c*p^c|basec=
n^(a+1)|basea+m^(b+1)|baseb=p^(c+1)|basec
n^(a+1)|basef*g+m^(b+1)|basef*h=p^(c+1)basef*k=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef=0
a,b,c..>impair,odd->((n^(a+1))^g),(m^(b+1))^h),(p^(c+1))^k) even
(((n^(a+1))^g+(m^(b+1))^h)-f*(p^(c+1))^k)=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef
[((((n^(a+1))^g+(m^(b+1))^h))]*f=(((n^(a+1))^g+(m^(b+1))^h)
f*g=a f*h=b f*k=c
by substituing:
[((((n^(f*g+1))^g+(m^(f*h+1))^h))]*f=(((n^(f*g+1))^g+(m^(f*h+1))^h)
f*n=n f*m=m g=a h=b k=c if (n^(1*g+1))^g=(m^(1*h+1))^h)) (g+1)^g)=(m+1)^h=(c+1))^k=i simplifies into last fermat theorem n^i+m^i=p^i
Power sum symmetric polynomial
From Wikipedia, the free encyclopedia
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Contents
[hide]
[edit]Definition
The power sum symmetric polynomial of degree k in n variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers of the variables. Formally,

The first few of these polynomials are


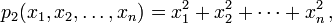

Thus, for each nonnegative integer k, there exists exactly one power sum symmetric polynomial of degree k in n variables.
The polynomial ring formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring.
[edit]Examples
The following lists the n power sum symmetric polynomials of positive degrees up to n for the first three positive values of n. In every case, p0 = n is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1:

For n = 2:
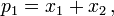

For n = 3:


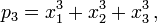
[edit]Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ring of symmetric polynomials in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) The same is true if the coefficients are taken in any field whose characteristic is 0.
The same is true if the coefficients are taken in any field whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
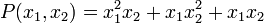
has the expression

which involves fractions. According to the theorem this is the only way to represent P(x1,x2) in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring ![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
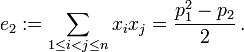
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then  , so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):

Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):

This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n. Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function  of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
[edit]References
- Macdonald, I.G. (1979), Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Oxford: Clarendon Press.
- Macdonald, I.G. (1995), Symmetric Functions and Hall Polynomials, second ed. Oxford: Clarendon Press. ISBN 0-19-850450-0 (paperback, 1998).
- Richard P. Stanley (1999), Enumerative Combinatorics, Vol. 2. Cambridge: Cambridge University Press. ISBN 0-521-56069-1
[edit]See also
Newton's identities
From Wikipedia, the free encyclopedia
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monicpolynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, includinggeneral relativity.
[edit]Mathematical statement
[edit]Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:

and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial that is the sum of all distinct products of k distinct variables, so in particular

Then the Newton's identities can be stated as

valid for all k ≥ 1. Concretely, one gets for the first few values of k:

The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has

and so on; here the left-hand sides never become zero. These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as

[edit]Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:
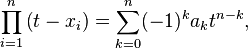
where the coefficients ak are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn). Now consider the power sums of the roots

Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
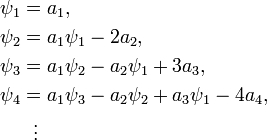
[edit]Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomial of a matrix A, the roots xi are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue xi of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is thek-th power sum ψk of the roots of the characteristic polynomial of A, is given by its trace:
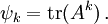
The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
[edit]Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomial expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial  with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
[edit]Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
[edit]A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomial that is the sum of all monomials of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functions, they read

valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has

These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity

The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
[edit]Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
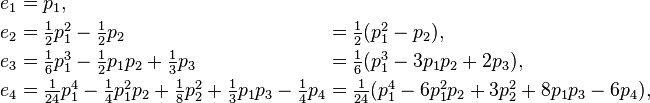
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
[edit]Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations

and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle index polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomialp1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as 1 / N where 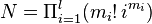 ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
[edit]Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators:
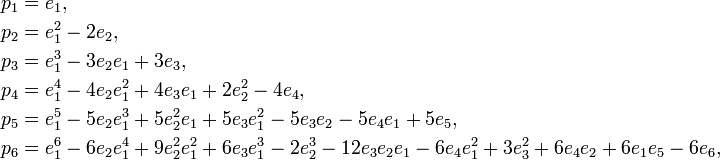
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial 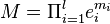 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
[edit]Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them:
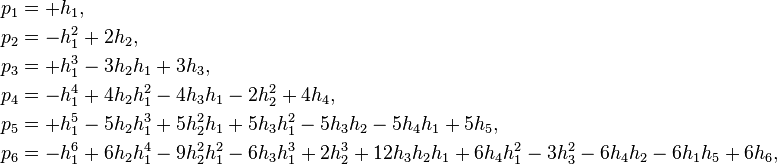
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial  is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
[edit]Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's rule to find the solution for the final unknown. For instance taking Newton's identities in the form
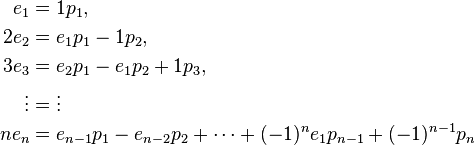
we consider p1, − p2, p3, ..., ( − 1)npn − 1 and pn as unknowns, and solve for the final one, giving

Solving for en instead of for pn is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
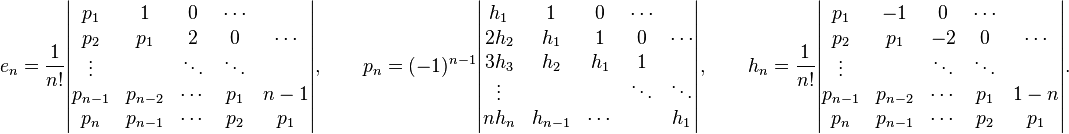
Note that the use of determinants makes that formula for hn has additional minus signs with respect to the one for en, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for hn by taking the permanent of the matrix for en instead of the determinant, and more generally an expression for any Schur polynomial can be obtained by taking the corresponding immanant of this matrix.
[edit]Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
[edit]From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into

as follows. Substituting xj for t gives

Summing over all j gives
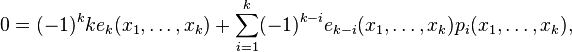
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
[edit]Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation

linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving

Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity

One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain

where the polynomial on the right hand side was first rewritten as a rational function in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains

which gives the k-th Newton identity.
[edit]As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomials of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has
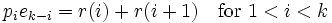
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially
 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus
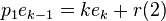 .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
[edit]See also
- Power sum symmetric polynomial
- Elementary symmetric polynomial
- Symmetric function
- Fluid solutions, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensor in the case of a perfect fluid, and similar articles on other types of exact solutions in general relativity.
[edit]References
- Tignol, Jean-Pierre (2001). Galois' theory of algebraic equations. Singapore: World Scientific. ISBN 978-981-02-4541-2.
- Bergeron, F.; Labelle, G.; and Leroux, P. (1998). Combinatorial species and tree-like structures. Cambridge: Cambridge University Press. ISBN 978-0-521-57323-8.
- Cameron, Peter J. (1999). Permutation Groups. Cambridge: Cambridge University Press. ISBN 978-0-521-65378-7.
- Cox, David; Little, John, and O'Shea, Donal (1992). Ideals, Varieties, and Algorithms. New York: Springer-Verlag. ISBN 978-0-387-97847-5.
- Eppstein, D.; Goodrich, M. T. (2007). "Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters". Algorithms and Data Structures, 10th International Workshop, WADS 2007. Springer-Verlag, Lecture Notes in Computer Science 4619. pp. 637–648. arXiv:0704.3313
- Littlewood, D. E. (1950). The theory of group characters and matrix representations of groups. Oxford: Oxford University Press. viii+310. ISBN 0-8218-4067-3.
- Macdonald, I. G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford: The Clarendon Press, Oxford University Press. viii+180. ISBN 0-19-853530-9. MR84g:05003
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (Second ed.). New York: Oxford Science Publications. The Clarendon Press, Oxford University Press. p. x+475. ISBN 0-19-853489-2.MR96h:05207
- Mead, D.G. (1992-10). "Newton's Identities". The American Mathematical Monthly (Mathematical Association of America) 99 (8): 749–751. doi:10.2307/2324242.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Vol. 2. Cambridge University Press. ISBN 0-521-56069-1 (hardback), ISBN 0-521-78987-7 (paperback).
- Sturmfels, Bernd (1992). Algorithms in Invariant Theory. New York: Springer-Verlag. ISBN 978-0-387-82445-1.
- Tucker, Alan (1980). Applied Combinatorics (5/e ed.). New York: Wiley. ISBN 978-0-471-73507-6.
[edit]External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine
THE BEAL CONJECTURE AND PRIZE
BEAL'S CONJECTURE: If Ax +By = Cz , where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
THE BEAL PRIZE. The conjecture and prize was announced in the December 1997 issue of the Notices of the American Mathematical Society. Since that time Andy Beal has increased the amount of the prize for his conjecture. The prize is now this: $100,000 for either a proof or a counterexample of his conjecture. The prize money is being held by the American Mathematical Society until it is awarded. In the meantime the interest is being used to fund some AMS activities and the annual Erdos Memorial Lecture.
CONDITIONS FOR WINNING THE PRIZE. The prize will be awarded by the prize committee appointed by the American Mathematical Society. The present committee members are Charles Fefferman, Ron Graham, and Dan Mauldin. The requirements for the award are that in the judgment of the committee, the solution has been recognized by the mathematics community. This includes that either a proof has been given and the result has appeared in a reputable refereed journal or a counterexample has been given and verified.
PRELIMINARY RESULTS. If you have believe you have solved the problem, please submit the solution to a reputable refereed journal. If you have questions, they can be mailed to:
The Beal Conjecture and Prize
c/o Professor R. Daniel Mauldin
Department of Mathematics
Box 311430
University of North Texas
Denton, Texas 76203
Questions and queries can also be FAXED to 940-565-4805 or sent by e-mail to
a_ntimes0|base a+b_mtimes0|baseb=c_ptimes0|basec
=a|base a*n+b|baseb*m=c|basec*p
a_atimes0|basen+b_btimes0|basem=c_timesc0|basep
a*n^a|basea+b*m^b|baseb-c*p^c|basec=
n^(a+1)|basea+m^(b+1)|baseb=p^(c+1)|basec
n^(a+1)|basef*g+m^(b+1)|basef*h=p^(c+1)basef*k=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef=0
a,b,c..>impair,odd->((n^(a+1))^g),(m^(b+1))^h),(p^(c+1))^k) even
(((n^(a+1))^g+(m^(b+1))^h)-f*(p^(c+1))^k)=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef
[((((n^(a+1))^g+(m^(b+1))^h))]*f=(((n^(a+1))^g+(m^(b+1))^h)
f*g=a f*h=b f*k=c
by substituing:
[((((n^(f*g+1))^g+(m^(f*h+1))^h))]*f=(((n^(f*g+1))^g+(m^(f*h+1))^h)
f*n=n f*m=m g=a h=b k=c if (n^(1*g+1))^g=(m^(1*h+1))^h)) (g+1)^g)=(m+1)^h=(c+1))^k=i simplifies into last fermat theorem n^i+m^i=p^i
Power sum symmetric polynomial
From Wikipedia, the free encyclopedia
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Contents
[hide]
[edit]Definition
The power sum symmetric polynomial of degree k in n variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers of the variables. Formally,

The first few of these polynomials are


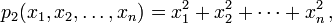

Thus, for each nonnegative integer k, there exists exactly one power sum symmetric polynomial of degree k in n variables.
The polynomial ring formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring.
[edit]Examples
The following lists the n power sum symmetric polynomials of positive degrees up to n for the first three positive values of n. In every case, p0 = n is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1:

For n = 2:
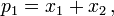

For n = 3:


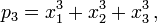
[edit]Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ring of symmetric polynomials in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) The same is true if the coefficients are taken in any field whose characteristic is 0.
The same is true if the coefficients are taken in any field whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
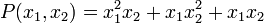
has the expression

which involves fractions. According to the theorem this is the only way to represent P(x1,x2) in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring ![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
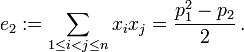
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then  , so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):

Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):

This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n. Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function  of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
[edit]References
- Macdonald, I.G. (1979), Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Oxford: Clarendon Press.
- Macdonald, I.G. (1995), Symmetric Functions and Hall Polynomials, second ed. Oxford: Clarendon Press. ISBN 0-19-850450-0 (paperback, 1998).
- Richard P. Stanley (1999), Enumerative Combinatorics, Vol. 2. Cambridge: Cambridge University Press. ISBN 0-521-56069-1
[edit]See also
Newton's identities
From Wikipedia, the free encyclopedia
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monicpolynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, includinggeneral relativity.
[edit]Mathematical statement
[edit]Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:

and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial that is the sum of all distinct products of k distinct variables, so in particular

Then the Newton's identities can be stated as

valid for all k ≥ 1. Concretely, one gets for the first few values of k:

The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has

and so on; here the left-hand sides never become zero. These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as

[edit]Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:
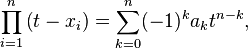
where the coefficients ak are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn). Now consider the power sums of the roots

Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
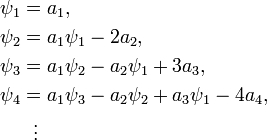
[edit]Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomial of a matrix A, the roots xi are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue xi of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is thek-th power sum ψk of the roots of the characteristic polynomial of A, is given by its trace:
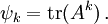
The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
[edit]Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomial expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial  with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
[edit]Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
[edit]A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomial that is the sum of all monomials of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functions, they read

valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has

These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity

The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
[edit]Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
[edit]Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations

and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle index polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomialp1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as 1 / N where  ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
[edit]Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators:
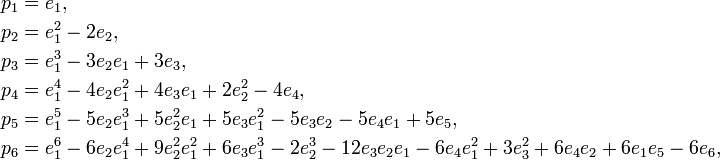
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial 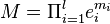 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
[edit]Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them:
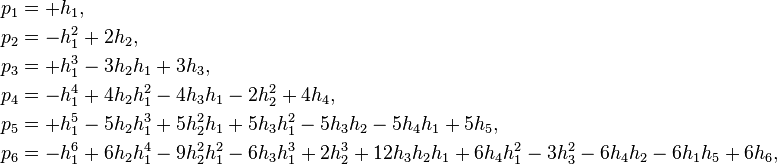
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial  is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
[edit]Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's rule to find the solution for the final unknown. For instance taking Newton's identities in the form
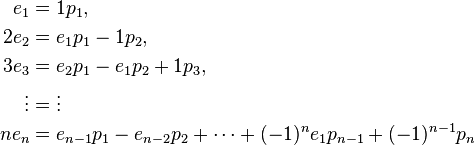
we consider p1, − p2, p3, ..., ( − 1)npn − 1 and pn as unknowns, and solve for the final one, giving

Solving for en instead of for pn is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
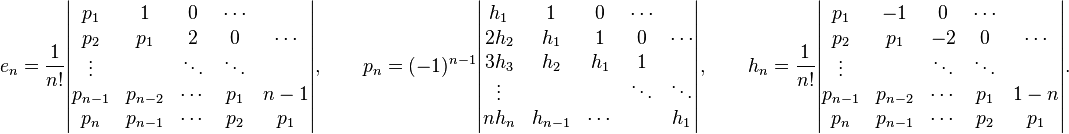
Note that the use of determinants makes that formula for hn has additional minus signs with respect to the one for en, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for hn by taking the permanent of the matrix for en instead of the determinant, and more generally an expression for any Schur polynomial can be obtained by taking the corresponding immanant of this matrix.
[edit]Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
[edit]From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into

as follows. Substituting xj for t gives

Summing over all j gives
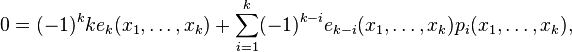
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
[edit]Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation

linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving

Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity

One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain

where the polynomial on the right hand side was first rewritten as a rational function in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains

which gives the k-th Newton identity.
[edit]As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomials of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has
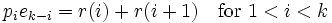
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially
 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus
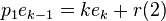 .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
[edit]See also
- Power sum symmetric polynomial
- Elementary symmetric polynomial
- Symmetric function
- Fluid solutions, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensor in the case of a perfect fluid, and similar articles on other types of exact solutions in general relativity.
[edit]References
- Tignol, Jean-Pierre (2001). Galois' theory of algebraic equations. Singapore: World Scientific. ISBN 978-981-02-4541-2.
- Bergeron, F.; Labelle, G.; and Leroux, P. (1998). Combinatorial species and tree-like structures. Cambridge: Cambridge University Press. ISBN 978-0-521-57323-8.
- Cameron, Peter J. (1999). Permutation Groups. Cambridge: Cambridge University Press. ISBN 978-0-521-65378-7.
- Cox, David; Little, John, and O'Shea, Donal (1992). Ideals, Varieties, and Algorithms. New York: Springer-Verlag. ISBN 978-0-387-97847-5.
- Eppstein, D.; Goodrich, M. T. (2007). "Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters". Algorithms and Data Structures, 10th International Workshop, WADS 2007. Springer-Verlag, Lecture Notes in Computer Science 4619. pp. 637–648. arXiv:0704.3313
- Littlewood, D. E. (1950). The theory of group characters and matrix representations of groups. Oxford: Oxford University Press. viii+310. ISBN 0-8218-4067-3.
- Macdonald, I. G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford: The Clarendon Press, Oxford University Press. viii+180. ISBN 0-19-853530-9. MR84g:05003
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (Second ed.). New York: Oxford Science Publications. The Clarendon Press, Oxford University Press. p. x+475. ISBN 0-19-853489-2.MR96h:05207
- Mead, D.G. (1992-10). "Newton's Identities". The American Mathematical Monthly (Mathematical Association of America) 99 (8): 749–751. doi:10.2307/2324242.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Vol. 2. Cambridge University Press. ISBN 0-521-56069-1 (hardback), ISBN 0-521-78987-7 (paperback).
- Sturmfels, Bernd (1992). Algorithms in Invariant Theory. New York: Springer-Verlag. ISBN 978-0-387-82445-1.
- Tucker, Alan (1980). Applied Combinatorics (5/e ed.). New York: Wiley. ISBN 978-0-471-73507-6.
[edit]External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine
THE BEAL CONJECTURE AND PRIZE
BEAL'S CONJECTURE: If Ax +By = Cz , where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
THE BEAL PRIZE. The conjecture and prize was announced in the December 1997 issue of the Notices of the American Mathematical Society. Since that time Andy Beal has increased the amount of the prize for his conjecture. The prize is now this: $100,000 for either a proof or a counterexample of his conjecture. The prize money is being held by the American Mathematical Society until it is awarded. In the meantime the interest is being used to fund some AMS activities and the annual Erdos Memorial Lecture.
CONDITIONS FOR WINNING THE PRIZE. The prize will be awarded by the prize committee appointed by the American Mathematical Society. The present committee members are Charles Fefferman, Ron Graham, and Dan Mauldin. The requirements for the award are that in the judgment of the committee, the solution has been recognized by the mathematics community. This includes that either a proof has been given and the result has appeared in a reputable refereed journal or a counterexample has been given and verified.
PRELIMINARY RESULTS. If you have believe you have solved the problem, please submit the solution to a reputable refereed journal. If you have questions, they can be mailed to:
The Beal Conjecture and Prize
c/o Professor R. Daniel Mauldin
Department of Mathematics
Box 311430
University of North Texas
Denton, Texas 76203
Questions and queries can also be FAXED to 940-565-4805 or sent by e-mail to
a_ntimes0|base a+b_mtimes0|baseb=c_ptimes0|basec
=a|base a*n+b|baseb*m=c|basec*p
a_atimes0|basen+b_btimes0|basem=c_timesc0|basep
a*n^a|basea+b*m^b|baseb-c*p^c|basec=
n^(a+1)|basea+m^(b+1)|baseb=p^(c+1)|basec
n^(a+1)|basef*g+m^(b+1)|basef*h=p^(c+1)basef*k=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef=0
a,b,c..>impair,odd->((n^(a+1))^g),(m^(b+1))^h),(p^(c+1))^k) even
(((n^(a+1))^g+(m^(b+1))^h)-f*(p^(c+1))^k)=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef
[((((n^(a+1))^g+(m^(b+1))^h))]*f=(((n^(a+1))^g+(m^(b+1))^h)
f*g=a f*h=b f*k=c
by substituing:
[((((n^(f*g+1))^g+(m^(f*h+1))^h))]*f=(((n^(f*g+1))^g+(m^(f*h+1))^h)
f*n=n f*m=m g=a h=b k=c if (n^(1*g+1))^g=(m^(1*h+1))^h)) (g+1)^g)=(m+1)^h=(c+1))^k=i simplifies into last fermat theorem n^i+m^i=p^i
Power sum symmetric polynomial
From Wikipedia, the free encyclopedia
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Contents
[hide]
[edit]Definition
The power sum symmetric polynomial of degree k in n variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers of the variables. Formally,

The first few of these polynomials are


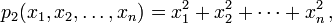

Thus, for each nonnegative integer k, there exists exactly one power sum symmetric polynomial of degree k in n variables.
The polynomial ring formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring.
[edit]Examples
The following lists the n power sum symmetric polynomials of positive degrees up to n for the first three positive values of n. In every case, p0 = n is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1:

For n = 2:
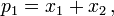

For n = 3:


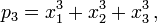
[edit]Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ring of symmetric polynomials in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) The same is true if the coefficients are taken in any field whose characteristic is 0.
The same is true if the coefficients are taken in any field whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
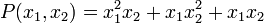
has the expression

which involves fractions. According to the theorem this is the only way to represent P(x1,x2) in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring ![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
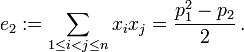
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then  , so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):

Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):

This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n. Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function  of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
[edit]References
- Macdonald, I.G. (1979), Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Oxford: Clarendon Press.
- Macdonald, I.G. (1995), Symmetric Functions and Hall Polynomials, second ed. Oxford: Clarendon Press. ISBN 0-19-850450-0 (paperback, 1998).
- Richard P. Stanley (1999), Enumerative Combinatorics, Vol. 2. Cambridge: Cambridge University Press. ISBN 0-521-56069-1
[edit]See also
Newton's identities
From Wikipedia, the free encyclopedia
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monicpolynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, includinggeneral relativity.
[edit]Mathematical statement
[edit]Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:

and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial that is the sum of all distinct products of k distinct variables, so in particular

Then the Newton's identities can be stated as

valid for all k ≥ 1. Concretely, one gets for the first few values of k:

The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has

and so on; here the left-hand sides never become zero. These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as

[edit]Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:
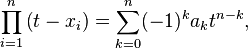
where the coefficients ak are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn). Now consider the power sums of the roots

Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
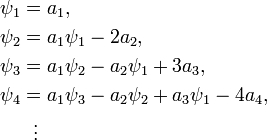
[edit]Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomial of a matrix A, the roots xi are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue xi of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is thek-th power sum ψk of the roots of the characteristic polynomial of A, is given by its trace:
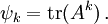
The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
[edit]Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomial expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial  with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
[edit]Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
[edit]A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomial that is the sum of all monomials of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functions, they read

valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has

These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity

The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
[edit]Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
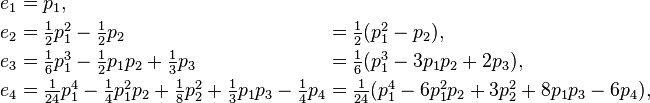
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
[edit]Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations

and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle index polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomialp1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as 1 / N where 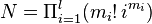 ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
[edit]Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators:
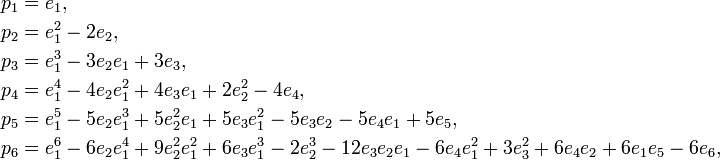
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial 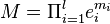 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
[edit]Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them:
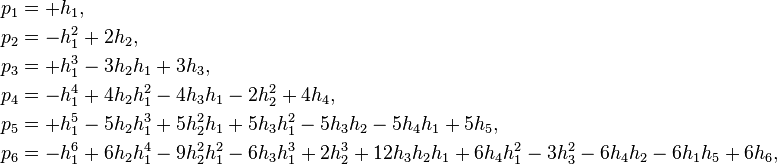
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial  is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
[edit]Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's rule to find the solution for the final unknown. For instance taking Newton's identities in the form
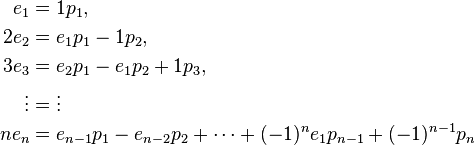
we consider p1, − p2, p3, ..., ( − 1)npn − 1 and pn as unknowns, and solve for the final one, giving

Solving for en instead of for pn is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
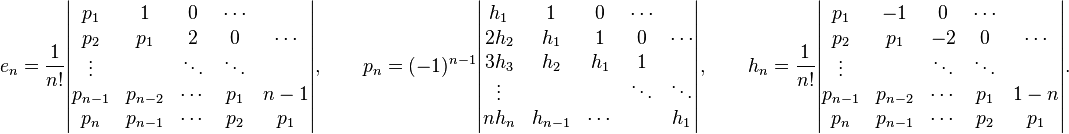
Note that the use of determinants makes that formula for hn has additional minus signs with respect to the one for en, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for hn by taking the permanent of the matrix for en instead of the determinant, and more generally an expression for any Schur polynomial can be obtained by taking the corresponding immanant of this matrix.
[edit]Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
[edit]From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into

as follows. Substituting xj for t gives

Summing over all j gives
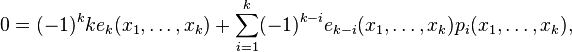
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
[edit]Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation

linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving

Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity

One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain

where the polynomial on the right hand side was first rewritten as a rational function in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains

which gives the k-th Newton identity.
[edit]As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomials of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has
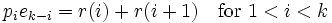
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially
 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus
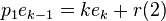 .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
[edit]See also
- Power sum symmetric polynomial
- Elementary symmetric polynomial
- Symmetric function
- Fluid solutions, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensor in the case of a perfect fluid, and similar articles on other types of exact solutions in general relativity.
[edit]References
- Tignol, Jean-Pierre (2001). Galois' theory of algebraic equations. Singapore: World Scientific. ISBN 978-981-02-4541-2.
- Bergeron, F.; Labelle, G.; and Leroux, P. (1998). Combinatorial species and tree-like structures. Cambridge: Cambridge University Press. ISBN 978-0-521-57323-8.
- Cameron, Peter J. (1999). Permutation Groups. Cambridge: Cambridge University Press. ISBN 978-0-521-65378-7.
- Cox, David; Little, John, and O'Shea, Donal (1992). Ideals, Varieties, and Algorithms. New York: Springer-Verlag. ISBN 978-0-387-97847-5.
- Eppstein, D.; Goodrich, M. T. (2007). "Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters". Algorithms and Data Structures, 10th International Workshop, WADS 2007. Springer-Verlag, Lecture Notes in Computer Science 4619. pp. 637–648. arXiv:0704.3313
- Littlewood, D. E. (1950). The theory of group characters and matrix representations of groups. Oxford: Oxford University Press. viii+310. ISBN 0-8218-4067-3.
- Macdonald, I. G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford: The Clarendon Press, Oxford University Press. viii+180. ISBN 0-19-853530-9. MR84g:05003
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (Second ed.). New York: Oxford Science Publications. The Clarendon Press, Oxford University Press. p. x+475. ISBN 0-19-853489-2.MR96h:05207
- Mead, D.G. (1992-10). "Newton's Identities". The American Mathematical Monthly (Mathematical Association of America) 99 (8): 749–751. doi:10.2307/2324242.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Vol. 2. Cambridge University Press. ISBN 0-521-56069-1 (hardback), ISBN 0-521-78987-7 (paperback).
- Sturmfels, Bernd (1992). Algorithms in Invariant Theory. New York: Springer-Verlag. ISBN 978-0-387-82445-1.
- Tucker, Alan (1980). Applied Combinatorics (5/e ed.). New York: Wiley. ISBN 978-0-471-73507-6.
[edit]External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine
THE BEAL CONJECTURE AND PRIZE
BEAL'S CONJECTURE: If Ax +By = Cz , where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
THE BEAL PRIZE. The conjecture and prize was announced in the December 1997 issue of the Notices of the American Mathematical Society. Since that time Andy Beal has increased the amount of the prize for his conjecture. The prize is now this: $100,000 for either a proof or a counterexample of his conjecture. The prize money is being held by the American Mathematical Society until it is awarded. In the meantime the interest is being used to fund some AMS activities and the annual Erdos Memorial Lecture.
CONDITIONS FOR WINNING THE PRIZE. The prize will be awarded by the prize committee appointed by the American Mathematical Society. The present committee members are Charles Fefferman, Ron Graham, and Dan Mauldin. The requirements for the award are that in the judgment of the committee, the solution has been recognized by the mathematics community. This includes that either a proof has been given and the result has appeared in a reputable refereed journal or a counterexample has been given and verified.
PRELIMINARY RESULTS. If you have believe you have solved the problem, please submit the solution to a reputable refereed journal. If you have questions, they can be mailed to:
The Beal Conjecture and Prize
c/o Professor R. Daniel Mauldin
Department of Mathematics
Box 311430
University of North Texas
Denton, Texas 76203
c/o Professor R. Daniel Mauldin
Department of Mathematics
Box 311430
University of North Texas
Denton, Texas 76203
Questions and queries can also be FAXED to 940-565-4805 or sent by e-mail to
a_ntimes0|base a+b_mtimes0|baseb=c_ptimes0|basec
=a|base a*n+b|baseb*m=c|basec*p
a_atimes0|basen+b_btimes0|basem=c_timesc0|basep
a_atimes0|basen+b_btimes0|basem=c_timesc0|basep
a*n^a|basea+b*m^b|baseb-c*p^c|basec=
n^(a+1)|basea+m^(b+1)|baseb=p^(c+1)|basec
n^(a+1)|basef*g+m^(b+1)|basef*h=p^(c+1)basef*k=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef=0
a,b,c..>impair,odd->((n^(a+1))^g),(m^(b+1))^h),(p^(c+1))^k) even
n^(a+1)|basea+m^(b+1)|baseb=p^(c+1)|basec
n^(a+1)|basef*g+m^(b+1)|basef*h=p^(c+1)basef*k=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef=0
a,b,c..>impair,odd->((n^(a+1))^g),(m^(b+1))^h),(p^(c+1))^k) even
(((n^(a+1))^g+(m^(b+1))^h)-f*(p^(c+1))^k)=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef
[((((n^(a+1))^g+(m^(b+1))^h))]*f=(((n^(a+1))^g+(m^(b+1))^h)
f*g=a f*h=b f*k=c
by substituing:
[((((n^(f*g+1))^g+(m^(f*h+1))^h))]*f=(((n^(f*g+1))^g+(m^(f*h+1))^h)
f*n=n f*m=m g=a h=b k=c if (n^(1*g+1))^g=(m^(1*h+1))^h)) (g+1)^g)=(m+1)^h=(c+1))^k=i simplifies into last fermat theorem n^i+m^i=p^i
Power sum symmetric polynomial
From Wikipedia, the free encyclopedia
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Contents
[hide]
[edit]Definition
The power sum symmetric polynomial of degree k in n variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers of the variables. Formally,

The first few of these polynomials are


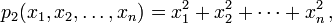

Thus, for each nonnegative integer k, there exists exactly one power sum symmetric polynomial of degree k in n variables.
The polynomial ring formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring.
[edit]Examples
The following lists the n power sum symmetric polynomials of positive degrees up to n for the first three positive values of n. In every case, p0 = n is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1:

For n = 2:
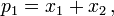

For n = 3:


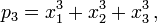
[edit]Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ring of symmetric polynomials in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) The same is true if the coefficients are taken in any field whose characteristic is 0.
The same is true if the coefficients are taken in any field whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
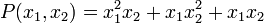
has the expression

which involves fractions. According to the theorem this is the only way to represent P(x1,x2) in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring ![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
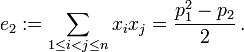
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then  , so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):

Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):

This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n. Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function  of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
[edit]References
- Macdonald, I.G. (1979), Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Oxford: Clarendon Press.
- Macdonald, I.G. (1995), Symmetric Functions and Hall Polynomials, second ed. Oxford: Clarendon Press. ISBN 0-19-850450-0 (paperback, 1998).
- Richard P. Stanley (1999), Enumerative Combinatorics, Vol. 2. Cambridge: Cambridge University Press. ISBN 0-521-56069-1
[edit]See also
Newton's identities
From Wikipedia, the free encyclopedia
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monicpolynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, includinggeneral relativity.
[edit]Mathematical statement
[edit]Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:

and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial that is the sum of all distinct products of k distinct variables, so in particular

Then the Newton's identities can be stated as

valid for all k ≥ 1. Concretely, one gets for the first few values of k:

The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has

and so on; here the left-hand sides never become zero. These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as

[edit]Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:
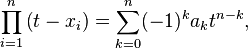
where the coefficients ak are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn). Now consider the power sums of the roots

Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
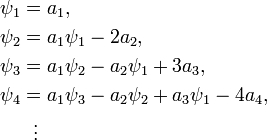
[edit]Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomial of a matrix A, the roots xi are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue xi of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is thek-th power sum ψk of the roots of the characteristic polynomial of A, is given by its trace:
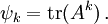
The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
[edit]Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomial expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial  with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
[edit]Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
[edit]A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomial that is the sum of all monomials of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functions, they read

valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has

These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity

The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
[edit]Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
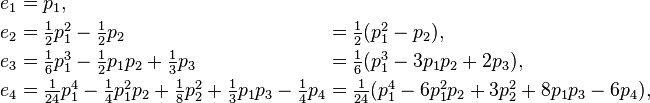
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
[edit]Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations

and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle index polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomialp1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as 1 / N where  ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
[edit]Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators:
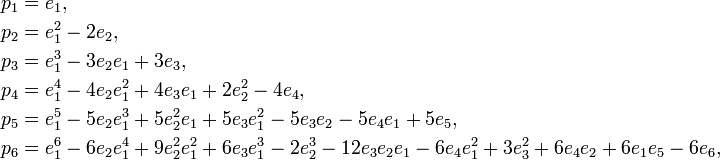
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial 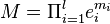 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
[edit]Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them:
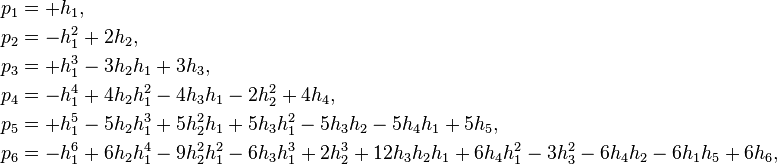
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial  is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
[edit]Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's rule to find the solution for the final unknown. For instance taking Newton's identities in the form
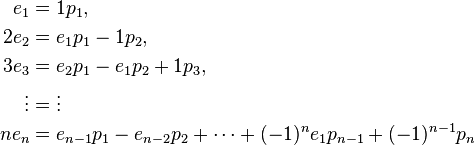
we consider p1, − p2, p3, ..., ( − 1)npn − 1 and pn as unknowns, and solve for the final one, giving

Solving for en instead of for pn is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
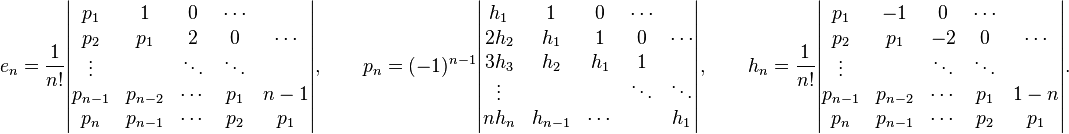
Note that the use of determinants makes that formula for hn has additional minus signs with respect to the one for en, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for hn by taking the permanent of the matrix for en instead of the determinant, and more generally an expression for any Schur polynomial can be obtained by taking the corresponding immanant of this matrix.
[edit]Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
[edit]From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into

as follows. Substituting xj for t gives

Summing over all j gives
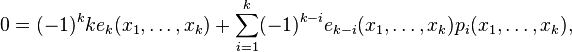
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
[edit]Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation

linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving

Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity

One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain

where the polynomial on the right hand side was first rewritten as a rational function in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains

which gives the k-th Newton identity.
[edit]As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomials of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has
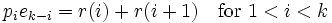
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially
 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus
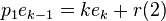 .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
[edit]See also
- Power sum symmetric polynomial
- Elementary symmetric polynomial
- Symmetric function
- Fluid solutions, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensor in the case of a perfect fluid, and similar articles on other types of exact solutions in general relativity.
[edit]References
- Tignol, Jean-Pierre (2001). Galois' theory of algebraic equations. Singapore: World Scientific. ISBN 978-981-02-4541-2.
- Bergeron, F.; Labelle, G.; and Leroux, P. (1998). Combinatorial species and tree-like structures. Cambridge: Cambridge University Press. ISBN 978-0-521-57323-8.
- Cameron, Peter J. (1999). Permutation Groups. Cambridge: Cambridge University Press. ISBN 978-0-521-65378-7.
- Cox, David; Little, John, and O'Shea, Donal (1992). Ideals, Varieties, and Algorithms. New York: Springer-Verlag. ISBN 978-0-387-97847-5.
- Eppstein, D.; Goodrich, M. T. (2007). "Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters". Algorithms and Data Structures, 10th International Workshop, WADS 2007. Springer-Verlag, Lecture Notes in Computer Science 4619. pp. 637–648. arXiv:0704.3313
- Littlewood, D. E. (1950). The theory of group characters and matrix representations of groups. Oxford: Oxford University Press. viii+310. ISBN 0-8218-4067-3.
- Macdonald, I. G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford: The Clarendon Press, Oxford University Press. viii+180. ISBN 0-19-853530-9. MR84g:05003
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (Second ed.). New York: Oxford Science Publications. The Clarendon Press, Oxford University Press. p. x+475. ISBN 0-19-853489-2.MR96h:05207
- Mead, D.G. (1992-10). "Newton's Identities". The American Mathematical Monthly (Mathematical Association of America) 99 (8): 749–751. doi:10.2307/2324242.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Vol. 2. Cambridge University Press. ISBN 0-521-56069-1 (hardback), ISBN 0-521-78987-7 (paperback).
- Sturmfels, Bernd (1992). Algorithms in Invariant Theory. New York: Springer-Verlag. ISBN 978-0-387-82445-1.
- Tucker, Alan (1980). Applied Combinatorics (5/e ed.). New York: Wiley. ISBN 978-0-471-73507-6.
[edit]External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine
(((n^(a+1))^g+(m^(b+1))^h)-f*(p^(c+1))^k)=
=(((n^(a+1))^g+(m^(b+1))^h)-(p^(c+1))^k)|basef
[((((n^(a+1))^g+(m^(b+1))^h))]*f=(((n^(a+1))^g+(m^(b+1))^h)
f*g=a f*h=b f*k=c
by substituing:
[((((n^(f*g+1))^g+(m^(f*h+1))^h))]*f=(((n^(f*g+1))^g+(m^(f*h+1))^h)
f*n=n f*m=m g=a h=b k=c if (n^(1*g+1))^g=(m^(1*h+1))^h)) (g+1)^g)=(m+1)^h=(c+1))^k=i simplifies into last fermat theorem n^i+m^i=p^i
Power sum symmetric polynomial
From Wikipedia, the free encyclopedia
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Contents[hide] |
[edit]Definition
The power sum symmetric polynomial of degree k in n variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers of the variables. Formally,
The first few of these polynomials are
Thus, for each nonnegative integer k, there exists exactly one power sum symmetric polynomial of degree k in n variables.
The polynomial ring formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring.
[edit]Examples
The following lists the n power sum symmetric polynomials of positive degrees up to n for the first three positive values of n. In every case, p0 = n is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1:
For n = 2:
For n = 3:
[edit]Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ring of symmetric polynomials in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) The same is true if the coefficients are taken in any field whose characteristic is 0.
The same is true if the coefficients are taken in any field whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
has the expression
which involves fractions. According to the theorem this is the only way to represent P(x1,x2) in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring ![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
![\mathbb Z[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/3/a/e/3aef60ed9bb797ef62960e407278b111.png) For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
For another example, the elementary symmetric polynomialsek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then  , so p1 and p2 cannot generate e2 = x1x2.
, so p1 and p2 cannot generate e2 = x1x2.
 , so p1 and p2 cannot generate e2 = x1x2.
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities):
Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):
This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n. Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function  of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
Because every power sum polynomial is symmetric, the two rings are equal.
 of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, ![\mathbb Q[p_1,\ldots,p_n].](http://upload.wikimedia.org/math/e/8/2/e82b72f6b738a3854cba3de282ee43d3.png) Because every power sum polynomial is symmetric, the two rings are equal.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomials.
[edit]References
- Macdonald, I.G. (1979), Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Oxford: Clarendon Press.
- Macdonald, I.G. (1995), Symmetric Functions and Hall Polynomials, second ed. Oxford: Clarendon Press. ISBN 0-19-850450-0 (paperback, 1998).
- Richard P. Stanley (1999), Enumerative Combinatorics, Vol. 2. Cambridge: Cambridge University Press. ISBN 0-521-56069-1
[edit]See also
Newton's identities
From Wikipedia, the free encyclopedia
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monicpolynomial P in one variable, they allow expressing the sums of the k-th powers of all roots of P (counted with their multiplicity) in terms of the coefficients of P, without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, includinggeneral relativity.
[edit]Mathematical statement
[edit]Formulation in terms of symmetric polynomials
Let x1,…, xn be variables, denote for k ≥ 1 by pk(x1,…,xn) the k-th power sum:
and for k ≥ 0 denote by ek(x1,…,xn) the elementary symmetric polynomial that is the sum of all distinct products of k distinct variables, so in particular
Then the Newton's identities can be stated as
valid for all k ≥ 1. Concretely, one gets for the first few values of k:
The form and validity of these equations do not depend on the number n of variables (although the point where the left-hand side becomes 0 does, namely after the n-th identity), which makes it possible to state them as identities in the ring of symmetric functions. In that ring one has
and so on; here the left-hand sides never become zero. These equations allow to recursively express the ei in terms of the pk; to be able to do the inverse, one may rewrite them as
[edit]Application to the roots of a polynomial
Now view the xi as parameters rather than as variables, and consider the monic polynomial in t with roots x1,…,xn:
where the coefficients ak are given by the elementary symmetric polynomials in the roots: ak = ek(x1,…,xn). Now consider the power sums of the roots
Then according to Newton's identities these can be expressed recursively in terms of the coefficients of the polynomial using
[edit]Application to the characteristic polynomial of a matrix
When the polynomial above is the characteristic polynomial of a matrix A, the roots xi are the eigenvalues of the matrix, counted with their algebraic multiplicity. For any positive integer k, the matrix Ak has as eigenvalues the powers xik, and each eigenvalue xi of A contributes its multiplicity to that of the eigenvalue xik of Ak. Then the coefficients of the characteristic polynomial of Ak are given by the elementary symmetric polynomials in those powers xik. In particular, the sum of the xik, which is thek-th power sum ψk of the roots of the characteristic polynomial of A, is given by its trace:
The Newton identities now relate the traces of the powers Ak to the coefficients of the characteristic polynomial of A. Using them in reverse to express the elementary symmetric polynomials in terms of the power sums, they can be used to find the characteristic polynomial by computing only the powers Ak and their traces.
[edit]Relation with Galois theory
For a given n, the elementary symmetric polynomials ek(x1,…,xn) for k = 1,…, n form an algebraic basis for the space of symmetric polynomials in x1,…. xn: every polynomial expression in the xi that is invariant under all permutations of those variables is given by a polynomial expression in those elementary symmetric polynomials, and this expression is unique up to equivalence of polynomial expressions. This is a general fact known as the fundamental theorem of symmetric polynomials, and Newton's identities provide explicit formulae in the case of power sum symmetric polynomials. Applied to the monic polynomial  with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
 with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
with all coefficients ak considered as free parameters, this means that every symmetric polynomial expression S(x1,…,xn) in its roots can be expressed instead as a polynomial expression P(a1,…,an) in terms of its coefficients only, in other words without requiring knowledge of the roots. This fact also follows from general considerations in Galois theory(one views the ak as elements of a base field, the roots live in an extension field whose Galois group permutes them according to the full symmetric group, and the field fixed under all elements of the Galois group is the base field).
The Newton identities also permit expressing the elementary symmetric polynomials in terms of the power sum symmetric polynomials, showing that any symmetric polynomial can also be expressed in the power sums. In fact the first n power sums also form an algebraic basis for the space of symmetric polynomials.
[edit]Related identities
There is a number of (families of) identities that, while they should be distinguished from Newton's identities, are very closely related to them.
[edit]A variant using complete homogeneous symmetric polynomials
Denoting by hk the complete homogeneous symmetric polynomial that is the sum of all monomials of degree k, the power sum polynomials also satisfy identities similar to Newton's identities, but not involving any minus signs. Expressed as identities of in the ring of symmetric functions, they read
valid for all k ≥ 1. Contrary to Newton's identities,the left-hand sides do not become zero for large k, and the right hand sides contain ever more nonzero terms. For the first few values of k one has
These relations can be justified by an argument analoguous to the one by comparing coefficients in power series given above, based in this case on the generating function identity
The other proofs given above of Newton's identities cannot be easily adapted to prove these variants of those identities.
[edit]Expressing elementary symmetric polynomials in terms of power sums
A mentioned, Newton's identities can be used to recursively express elementary symmetric polynomials in terms of power sums. Doing so requires the introduction of integer denominators, so it can be done in the ring ΛQ of symmetric functions with rational coefficients:
and so forth. Applied to a monic polynomial these formulae express the coefficients in terms of the power sums of the roots: replace each ei by ai and each pk by ψk.
[edit]Expressing complete homogeneous symmetric polynomials in terms of power sums
The analogous relations involving complete homogeneous symmetric polynomials can be similarly developed, giving equations
and so forth, in which there are only plus signs. These expressions correspond exactly to the cycle index polynomials of the symmetric groups, if one interprets the power sums pi as indeterminates: the coefficient in the expression for hk of any monomialp1m1p2m2…plml is equal to the fraction of all permutations of k that have m1 fixed points, m2 cycles of length 2, …, and ml cycles of length l. Explicitly, this coefficient can be written as 1 / N where 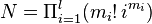 ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
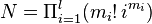 ; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….
; this N is the number permutations commuting with any given permutation π of the given cycle type. The expressions for the elementary symmetric functions have coefficients with the same absolute value, but a sign equal to the sign of π, namely (−1)m2+m4+….[edit]Expressing power sums in terms of elementary symmetric polynomials
One may also use Newton's identities to express power sums in terms of symmetric polynomials, which does not introduce denominators:
giving ever longer expressions that do not seem to follow any simple pattern. By consideration of the relations used to obtain these expressions, it can however be seen that the coefficient of some monomial 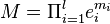 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
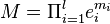 in the expression for pkhas the same sign as the coefficient of the corresponding product
in the expression for pkhas the same sign as the coefficient of the corresponding product  in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of
in the expression for ek described above, namely the sign (−1)m2+m4+…. Furthermore the absolute value of the coefficient of M is the sum, over all distinct sequences of elementary symmetric functions whose product is M, of the index of the last one in the sequence: for instance the coefficent of  in the expression for p20 will be
in the expression for p20 will be  , since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.
, since of all distinct orderings of the five factors e1, one factor e3 and three factors e4, there are 280 that end with e1, 56 that end with e3, and 168 that end with e4.[edit]Expressing power sums in terms of complete homogeneous symmetric polynomials
Finally one may use the variant identities involving complete homogeneous symmetric polynomials similarly to express power sums in term of them:
and so on. Apart from the replacement of each ei by the corresponding hi, the only change with respect to the previous family of identities is in the signs of the terms, which in this case depend just on the number of factors present: the sign of the monomial  is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
 is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.
is −(−1)m1+m2+m3+…. In particular the above description of the absolute value of the coefficients applies here as well.[edit]Expressions as determinants
One can obtain explicit formulas for the above expressions in the form of determinants, by considering the first n of Newton's identities (or it counterparts for the complete homogeneous polynomials) as linear equations in which the elementary symmetric functions are known and the power sums are unknowns (or vice versa), and apply Cramer's rule to find the solution for the final unknown. For instance taking Newton's identities in the form
we consider p1, − p2, p3, ..., ( − 1)npn − 1 and pn as unknowns, and solve for the final one, giving
Solving for en instead of for pn is similar, as the analogous computations for the complete homogeneous symmetric polynomials; in each case the details are slightly messier than the final results, which are (Macdonald 1979, p. 20):
Note that the use of determinants makes that formula for hn has additional minus signs with respect to the one for en, while the situation for the expanded form given earlier is opposite. As remarked in (Littelwood 1950, p. 84) one can alternatively obtain the formula for hn by taking the permanent of the matrix for en instead of the determinant, and more generally an expression for any Schur polynomial can be obtained by taking the corresponding immanant of this matrix.
[edit]Derivation of the identities
Each of Newton's identities can easily be checked by elementary algebra; however, their validity in general needs a proof. Here are some possible derivations
[edit]From the special case n = k
One can obtain the k-th Newton identity in k variables by substitution into
as follows. Substituting xj for t gives
Summing over all j gives
where the terms for i = 0 were taken out of the sum because p0 is (usually) not defined. This equation immediately gives the k-th Newton identity in k variables. Since this is an identity of symmetric polynomials (homogeneous) of degree k, its validity for any number of variables follows from its validity for k variables. Concretely, the identities in n < k variables can be deduced by setting k − n variables to zero. The k-th Newton identity in n > k variables contains more terms on both sides of the equation than the one in k variables, but its validity will be assured if the coefficients of any monomial match. Because no individual monomial involves more than k of the variables, the monomial will survive the substitution of zero for some set of n − k (other) variables, after which the equality of coefficients is one that arises in the k-th Newton identity in k (suitably chosen) variables.
[edit]Comparing coefficients in series
A derivation can be given by formal manipulations based on the basic relation
linking roots and coefficients of a monic polynomial. However, to facilitate the manipulations one first "reverses the polynomials" by substituting 1/t for t and then multiplying both sides by tn to remove negative powers of t, giving
Swapping sides and expressing the ai as the elementary symmetric polynomials they stand for gives the identity
One differentiates both sides with respect to t, and then (for convenience) multiplies by t, to obtain
where the polynomial on the right hand side was first rewritten as a rational function in order to be able to factor out a product from of the summation, then the fraction in the summand was developed as a series in t, and finally the coefficient of each t j was collected, giving a power sum. (The series in t is a formal power series, but may alternatively be thought of as a series expansion for t sufficiently close to 0, for those more comfortable with that; in fact one is not interested in the function here, but only in the coefficients of the series.) Comparing coefficients of tk on both sides one obtains
which gives the k-th Newton identity.
[edit]As a telescopic sum of symmetric function identities
The following derivation, given essentially in (Mead, 1992), is formulated in the ring of symmetric functions for clarity (all identities are independent of the number of variables). Fix some k > 0, and define the symmetric function r(i) for 2 ≤ i ≤ k as the sum of all distinct monomials of degree k obtained by multiplying one variable raised to the power i with k − i distinct other variables (this is the monomial symmetric function mγ where γ is a hook shape (i,1,1,…1)). In particular r(k) = pk; for r(1) the description would amount to that of ek, but this case was excluded since here monomials no longer have any distinguished variable. All products piek−i can be expressed in terms of the r(j) with the first and last case being somewhat special. One has
since each product of terms on the left involving distinct variables contributes to r(i), while those where the variable from pi already occurs among the variables of the term from ek−i contributes to r(i + 1), and all terms on the right are so obtained exactly once. For i = k one multiplies by e0 = 1, giving trivially
 .
.
Finally the product p1ek−1 for i = 1 gives contributions to r(i + 1) = r(2) like for other values i < k, but the remaining contributions produce k times each monomial of ek, since any on of the variables may come from the factor p1; thus
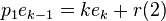 .
.
The k-th Newton identity is now obtained by taking the alternating sum of these equations, in which all terms of the form r(i) cancel out.
[edit]See also
- Power sum symmetric polynomial
- Elementary symmetric polynomial
- Symmetric function
- Fluid solutions, an article giving an application of Newton's identities to computing the characteristic polynomial of the Einstein tensor in the case of a perfect fluid, and similar articles on other types of exact solutions in general relativity.
[edit]References
- Tignol, Jean-Pierre (2001). Galois' theory of algebraic equations. Singapore: World Scientific. ISBN 978-981-02-4541-2.
- Bergeron, F.; Labelle, G.; and Leroux, P. (1998). Combinatorial species and tree-like structures. Cambridge: Cambridge University Press. ISBN 978-0-521-57323-8.
- Cameron, Peter J. (1999). Permutation Groups. Cambridge: Cambridge University Press. ISBN 978-0-521-65378-7.
- Cox, David; Little, John, and O'Shea, Donal (1992). Ideals, Varieties, and Algorithms. New York: Springer-Verlag. ISBN 978-0-387-97847-5.
- Eppstein, D.; Goodrich, M. T. (2007). "Space-efficient straggler identification in round-trip data streams via Newton's identities and invertible Bloom filters". Algorithms and Data Structures, 10th International Workshop, WADS 2007. Springer-Verlag, Lecture Notes in Computer Science 4619. pp. 637–648. arXiv:0704.3313
- Littlewood, D. E. (1950). The theory of group characters and matrix representations of groups. Oxford: Oxford University Press. viii+310. ISBN 0-8218-4067-3.
- Macdonald, I. G. (1979). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs. Oxford: The Clarendon Press, Oxford University Press. viii+180. ISBN 0-19-853530-9. MR84g:05003
- Macdonald, I. G. (1995). Symmetric functions and Hall polynomials. Oxford Mathematical Monographs (Second ed.). New York: Oxford Science Publications. The Clarendon Press, Oxford University Press. p. x+475. ISBN 0-19-853489-2.MR96h:05207
- Mead, D.G. (1992-10). "Newton's Identities". The American Mathematical Monthly (Mathematical Association of America) 99 (8): 749–751. doi:10.2307/2324242.
- Stanley, Richard P. (1999). Enumerative Combinatorics, Vol. 2. Cambridge University Press. ISBN 0-521-56069-1 (hardback), ISBN 0-521-78987-7 (paperback).
- Sturmfels, Bernd (1992). Algorithms in Invariant Theory. New York: Springer-Verlag. ISBN 978-0-387-82445-1.
- Tucker, Alan (1980). Applied Combinatorics (5/e ed.). New York: Wiley. ISBN 978-0-471-73507-6.
[edit]External links
- Newton–Girard formulas on MathWorld
- A Matrix Proof of Newton's Identities in Mathematics Magazine